Question

【题目】如图，抛物线与轴交于点，交轴于点，直线过点与轴交于点，与抛物线的另一个交点为，作轴于点.设点是直线上方的抛物线上一动点（不与点、重合），过点作轴的平行线，交直线于点，作于点.

（1）填空：__________，__________，__________；

（2）探究：是否存在这样的点，使四边形是平行四边形？若存在，请求出点的坐标；若不存在，请说明理由；

（3）设的周长为，点的横坐标为，求与的函数关系式，并求出的最大值.

Answer 1

【答案】（1），，；（2）存在，点的坐标是和；（3），的最大值是15.

【解析】

（1）将A，B两点分别代入y=x2+bx+c求出b，c，将A代入y=kx-求出k；
（2）首先假设出P，M点的坐标，进而得出PM的长，将两函数联立得出D点坐标，进而得出CE的长，利用平行四边形的判定得出PM=CE时四边形PMEC是平行四边形，得出等式方程求解并判断即可；
（3）利用勾股定理得出DC的长，进而根据△PMN∽△DCE，得出两三角形周长之比，求出l与x的函数关系，再利用配方法求出二次函数最值即可．

解：（1）：（1）把A（2，0），B（0，）代入y=x2+bx+c得 ，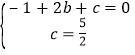

解得；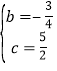
把A（2，0）代入y=kx-得2k-=0，解得k=，
∴，，，

（2）设的坐标是，则的坐标是，

∴ ，

解方程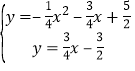，得：，，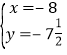

∵点在第三象限，则点的坐标是，

由得点的坐标是，

∴，

由于轴，所以当时四边形是平行四边形.

即，

解这个方程得：，，符合，

当时，，当时，，

综上所述：点的坐标是和；

（3）在中，，

由勾股定理得：

∴的周长是24，

∵轴，∴，

∴，即

化简整理得：与的函数关系式是：，

，

∵，∴当时，的最大值是15.