Question

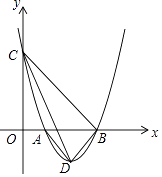
【题目】如图，垂直于x轴的直线AB分别与抛物线C1：y=x2（x≥0）和抛物线C2：y= （x≥0）交于A，B两点，过点A作CD∥x轴分别与y轴和抛物线C2交于点C，D，过点B作EF∥x轴分别与y轴和抛物线C1交于点E，F，则 的值为（ ）
A.
B.
C.
D.

Answer 1

【答案】D
【解析】解：设点A、B横坐标为a，则点A纵坐标为a2 ， 点B的纵坐标为 ， ∵BE∥x轴，
∴点F纵坐标为 ，
∵点F是抛物线y=x2上的点，
∴点F横坐标为x= = ，
∵CD∥x轴，∴点D纵坐标为a2 ，
∵点D是抛物线y= 上的点，
∴点D横坐标为x= =2a，
∴AD=a，BF= a，CE= a2 ， OE= a2 ，
∴则 = = × = ，
故选 D．
可以设A、B横坐标为a，易求得点E、F、D的坐标，即可求得OE、CE、AD、BF的长度，即可解题．