题目内容
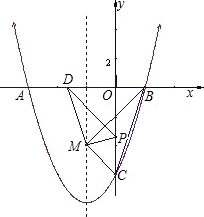 如图,已知抛物线y=ax2+bx+c(a≠0)与x轴交于A(-6,0)、B(2,0),与y轴交于点C(0,-6).
如图,已知抛物线y=ax2+bx+c(a≠0)与x轴交于A(-6,0)、B(2,0),与y轴交于点C(0,-6).(1)求此抛物线的函数表达式,写出它的对称轴;
(2)若在抛物线的对称轴上存在一点M,使△MBC的周长最小,求点M的坐标;
(3)若点P(0,k)为线段OC上的一个不与端点重合的动点,过点P作PD∥CM交x于点D,连接MD、MP,设△MPD的面积为S,求当点P运动到何处时S的值最大?
分析:(1)将A、B、C的坐标分别代入抛物线的解析式中,通过联立方程组即可求出待定系数的值;
(2)由于BC的长为定值,若△MBC的周长最小,那么MB+MC的值最小;由于A、B关于抛物线的对称轴对称,若连接AC,那么AC与抛物线对称轴的交点即为所求的M点;可先求出直线AC的解析式,然后联立抛物线的对称轴方程,即可求出M点的坐标;
(3)若DP∥MC,则△ODP∽△OAC,可设出P点的纵坐标,根据相似三角形的比例线段即可求出OD的长,那么三角形DMP的面积可由△OAC、△ADM、△MPC、△ODP的面积差求得,由此可得到关于S与P点纵坐标的函数关系式,根据所得函数的性质即可求得S的最大值及对应的P点坐标.
(2)由于BC的长为定值,若△MBC的周长最小,那么MB+MC的值最小;由于A、B关于抛物线的对称轴对称,若连接AC,那么AC与抛物线对称轴的交点即为所求的M点;可先求出直线AC的解析式,然后联立抛物线的对称轴方程,即可求出M点的坐标;
(3)若DP∥MC,则△ODP∽△OAC,可设出P点的纵坐标,根据相似三角形的比例线段即可求出OD的长,那么三角形DMP的面积可由△OAC、△ADM、△MPC、△ODP的面积差求得,由此可得到关于S与P点纵坐标的函数关系式,根据所得函数的性质即可求得S的最大值及对应的P点坐标.
解答: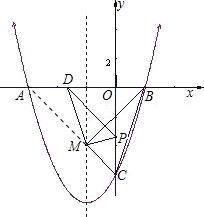 解:(1)抛物线与y轴交于点C(0,-6),
解:(1)抛物线与y轴交于点C(0,-6),
∴c=-6;
而抛物线过点A(-6,0)、B(2,0),
∴
;
解得a=
,b=2,
即此抛物线的函数表达式为y=
x2+2x-6;
它的对称轴为直线x=-2;
(2)∵A、B关于对称轴直线x=-2对称,M在对称轴上,
∴AM=BM;
所以当点A,M,C共线时,△MBC的周长最小;
直线AC的解析式是:y=-x-6,
令x=-2,得y=-4,
即点M的坐标为(-2,-4);
(3)点P(0,k)为线段OC上的一个不与端点重合的动点,
∴-6<k<0;
∵PD∥CM,
∴∠ODP=∠OAC,∠OPD=∠OCA,
∴△ODP∽△OAC,
∴
=
,
而OA=OC,
∴OD=OP,即D(k,0);
∴△MPD的面积S=S△AOC-S△AMD-S△MCP-S△POD;
即S=
×6×6-
×(6+k)×4-
×(6+k)×2-
×|k|2=-
k2-3k;
当k=-3时,S的值最大,最大值为
.
 解:(1)抛物线与y轴交于点C(0,-6),
解:(1)抛物线与y轴交于点C(0,-6),∴c=-6;
而抛物线过点A(-6,0)、B(2,0),
∴
|
解得a=
| 1 |
| 2 |
即此抛物线的函数表达式为y=
| 1 |
| 2 |
它的对称轴为直线x=-2;
(2)∵A、B关于对称轴直线x=-2对称,M在对称轴上,
∴AM=BM;
所以当点A,M,C共线时,△MBC的周长最小;
直线AC的解析式是:y=-x-6,
令x=-2,得y=-4,
即点M的坐标为(-2,-4);
(3)点P(0,k)为线段OC上的一个不与端点重合的动点,
∴-6<k<0;
∵PD∥CM,
∴∠ODP=∠OAC,∠OPD=∠OCA,
∴△ODP∽△OAC,
∴
| OD |
| OA |
| OP |
| OC |
而OA=OC,
∴OD=OP,即D(k,0);
∴△MPD的面积S=S△AOC-S△AMD-S△MCP-S△POD;
即S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
当k=-3时,S的值最大,最大值为
| 9 |
| 2 |
点评:此题主要考查了二次函数解析式的确定、轴对称的性质、相似三角形的判定和性质、图形面积的求法以及二次函数最值的应用等重要知识点,能够结合轴对称的性质和两点间线段最短的知识来确定点M的位置是解答此题的关键.

练习册系列答案
相关题目
 C(0,3).
C(0,3). 、C(0,-3)两点,与x轴交于另一点B.
、C(0,-3)两点,与x轴交于另一点B. (2013•衡阳)如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是x=-1.
(2013•衡阳)如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是x=-1. 如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,且抛物线经过A(-1,0)、C(0,-3)两点,与x轴交于另一点B.
如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,且抛物线经过A(-1,0)、C(0,-3)两点,与x轴交于另一点B. 如图,已知抛物线y=ax2+bx+c的顶点是(-1,-4),且与x轴交于A、B(1,0)两点,交y轴于点C;
如图,已知抛物线y=ax2+bx+c的顶点是(-1,-4),且与x轴交于A、B(1,0)两点,交y轴于点C;