Question

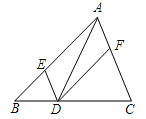
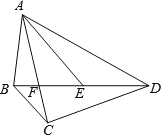
【题目】如图，四边形ABCD的对角线AC，BD交于点F，点E是BD上一点，且∠BAC＝∠BDC＝∠DAE．

（1）求证：△ABE∽△ACD；

（2）若BC＝2，AD＝6，DE＝3，求AC的长．

Answer 1

【答案】（1）见解析 （2）AC=4

【解析】

试题（1）根据∠BAC＝∠DAE得到∠BAE＝∠CAD，根据∠BAC＝∠BDC，∠BFA＝∠CFD得到∠ABE＝∠ACD，从而说明△ABE和△ACD相似；（2）根据△ABE∽△ACD得到＝，再根据∠BAC＝∠DAE得到△ABC和△AED相似，根据相似比求出AC的值.

试题解析：（1）∵∠BAC＝∠DAE，∴∠BAC＋∠CAE＝∠DAE＋∠CAE，即∠BAE＝∠CAD．

又∵∠BAC＝∠BDC，∠BFA＝∠CFD， ∴180°－∠BAC－∠BFA＝180°－∠BDC－∠CFD，即∠ABE＝∠ACD．

∴△ABE∽△ACD．

（2）∵△ABE∽△ACD，∴＝． 又∵∠BAC＝∠DAE， ∴△ABC∽△AED，

∴＝， ∴AC＝＝＝4．