题目内容
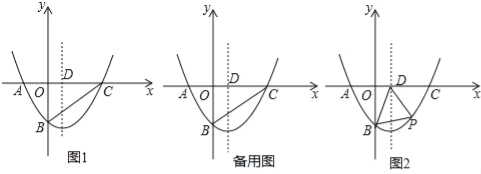
【题目】已知边长为3的正方形ABCD中,点E在射线BC上,且BE=2CE,连接AE交射线DC于点F,若△ABE沿直线AE翻折,点B落在点B1处.
(1)如图1,若点E在线段BC上,求CF的长;
(2)求sin∠DAB1的值;
(3)如果题设中“BE=2CE”改为“![]() =x”,其它条件都不变,试写出△ABE翻折后与正方形ABCD公共部分的面积y与x的关系式及自变量x的取值范围(只要写出结论,不需写出解题过程).
=x”,其它条件都不变,试写出△ABE翻折后与正方形ABCD公共部分的面积y与x的关系式及自变量x的取值范围(只要写出结论,不需写出解题过程).
【答案】(1)![]() ;(2) ①
;(2) ①![]() , ②
, ②![]() ;(3)见解析.
;(3)见解析.
【解析】分析:(1)利用平行线性质以及线段比求出CF的值;
(2)本题要分两种方法讨论:①若点E在线段BC上;②若点E在边BC的延长线上.需运用勾股定理求出与之相联的线段;
(3)本题分两种情况讨论:若点E在线段BC上,y=![]() ,自变量取值范围为x>0;若点E在边BC的延长线上,y=
,自变量取值范围为x>0;若点E在边BC的延长线上,y=![]() ,自变量取值范围为x>1.
,自变量取值范围为x>1.
详解:(1)∵AB∥DF,
∴![]() ,
,
∵BE=2CE,AB=3,
∴![]() ,
,
∴CF=![]() ;
;
(2)①若点E在线段BC上,如图1,设直线AB1与DC相交于点M.
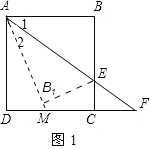
由题意翻折得:∠1=∠2.
∵AB∥DF,
∴∠1=∠F,
∴∠2=∠F,
∴AM=MF.
设DM=x,则CM=3-x.
又∵CF=1.5,
∴AM=MF=![]() -x,
-x,
在Rt△ADM中,AD2+DM2=AM2,
∴32+x2=(![]() -x)2,
-x)2,
∴x=![]() ,
,
∴DM=![]() ,AM=
,AM=![]() ,
,
∴sin∠DAB1=![]() ;
;
②若点E在边BC的延长线上,如图2,设直线AB1与CD延长线相交于点N.

同理可得:AN=NF.
∵BE=2CE,
∴BC=CE=AD.
∵AD∥BE,
∴![]() ,
,
∴DF=FC=![]() ,
,
设DN=x,则AN=NF=x+![]() .
.
在Rt△ADN中,AD2+DN2=AN2,
∴32+x2=(x+![]() )2,
)2,
∴x=![]() .
.
∴DN=![]() ,AN=
,AN=![]() ,sin∠DAB1=
,sin∠DAB1=![]() ;
;
(3)y=![]() ,自变量取值范围为x>0;若点E在边BC的延长线上,y=
,自变量取值范围为x>0;若点E在边BC的延长线上,y=![]() ,自变量取值范围为x>1.
,自变量取值范围为x>1.