题目内容
已知二次函数y=ax2+bx+c的图象的顶点坐标为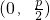 ,且
,且 .
.
(1)若该函数的图象经过点(-1,-1).
①求使y<0成立的x的取值范围.
②若圆心在该函数的图象上的圆与x轴、y轴都相切,求圆心的坐标.
(2)经过A(0,p)的直线与该函数的图象相交于M,N两点,过M,N作x轴的垂线,垂足分别为M1,N1,设△MAM1,△AM1N1,△ANN1的面积分别为S1,S2,S3,是否存在m,使得对任意实数p≠0都有S22=mS1S3成立?若存在,求出m的值,若不存在,请说明理由.
 解:(1)∵二次函数y=ax2+bx+c的图象的顶点坐标为
解:(1)∵二次函数y=ax2+bx+c的图象的顶点坐标为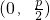 ,且
,且 ,
,又∵函数的图象经过点(-1,-1),
代入二次函数解析式得:
 ,
,解得:
 ,
,y=-
 x2-
x2- ,
,①利用函数图象可知使y<0成立的x的取值范围是:全体实数;
②若圆心在该函数的图象上的圆与x轴、y轴都相切,
假设与x轴切点为Q,与y轴切点为F,
∴OQ=FO,
∴-x=-
 x2-
x2- ,
,整理得:x2-2x+1=0,
解得:x1=x2=1,
∴QO=FO=1,
∴圆心的坐标为:(1,-1)或(-1,-1);
(2)二次函数y=ax2+bx+c的图象的顶点坐标为
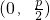 ,且
,且 .
.∴该二次函数的解析式为:y=
 x2+
x2+ ,
,∵过点A的直线与函数y=
 x2+
x2+ 的图象交于M(x1,y1),N(x2,y2),
的图象交于M(x1,y1),N(x2,y2),∴过点A的直线对应的函数为y=kx+p,
S1=
 |x1|•|y1|,
|x1|•|y1|,S2=
 |x1-x2|•|p|,
|x1-x2|•|p|,S3=
 |x2||y2|,
|x2||y2|,把y=kx+p代入y=
 x2+
x2+ 得,x2-2pkx-p2=0,
得,x2-2pkx-p2=0,∴x1+x2=2pk,x1x2=-p2,
∴S1S3=
 |x1x2y1y2|=
|x1x2y1y2|= p2|(kx2+p)(kx2+p)|=
p2|(kx2+p)(kx2+p)|= p4(k2+1),
p4(k2+1),S22=
 (x2-x1)2p2=p4(k2+1).
(x2-x1)2p2=p4(k2+1).∴4S1S3=S22,故存在m=4,使得对任意实数p≠0成立.
分析:(1)根据二次函数y=ax2+bx+c的图象的顶点坐标为
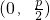 ,且
,且 ,以及函数的图象经过点(-1,-1),得出关于a,b,c的方程组,解方程组求出a,b,c的值.
,以及函数的图象经过点(-1,-1),得出关于a,b,c的方程组,解方程组求出a,b,c的值.①画出图象,即可得出使y<0成立的x的取值范围;
②根据圆与直线相切得出OQ=FO,再解一元二次方程即可得出;
(2)分别过M,N作直线l:y=-1的垂线,垂足分别是M1和N1.分别表示出△MAM1,△AM1N1,△ANN1的面积S1,S2,S3再条件S22=mS1S3成立进而求出m的值.
点评:此题主要考查了二次函数的综合应用以及圆的切线性质和三角形面积求法,二次函数的综合应用是初中阶段的重点题型特别注意利用数形结合是这部分考查的重点也是难点同学们应重点掌握.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知二次函数y=ax+bx+c(a≠0,a,b,c为常数),对称轴为直线x=1,它的部分自变量与函数值y的对应值如下表,写出方程ax2+bx+c=0的一个正数解的近似值________(精确到0.1).
| x | -0.1 | -0.2 | -0.3 | -0.4 |
| y=ax2+bx+c | -0.58 | -0.12 | 0.38 | 0.92 |
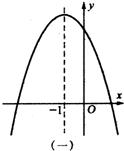 21、已知二次函数y=a(x+1)2+c的图象如图所示,则函数y=ax+c的图象只可能是( )
21、已知二次函数y=a(x+1)2+c的图象如图所示,则函数y=ax+c的图象只可能是( )
