题目内容
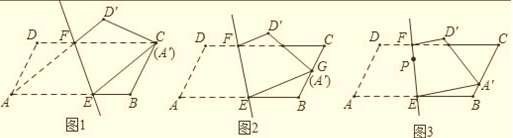
【题目】直线EF分别平行四边形ABCD边AB、 CD于点E、F，将图形沿直线EF对折，点A、D分别落在点、A'，D'处，
(1) 如图1，当点A’与点C重合时，连接AF，求证:四边形AECF是菱形:
(2)若∠A=60°，AD=4， AB=8,
①如图2.当点A’与BC边的中点G重合时，求AE的长；
②如图3.当点A’落在BC边上任意点时，设点P为直线EF上的动点，请直接写出PC+PA’的最小值 ;
【答案】（1）见解析；（2）①AE=
；②
【解析】
(1)先证明四边形AECF是平行四边形，再由翻折得AF=CF,则四边形AFCE是菱形；
(2)①如图2中，作
H⊥AB交AB的延长线于H，首先求出GH、BH，设AE=EG=x，在Rt△EGH中，根据
构建方程即可解决问题；
②如图3中，连接AC交EF于
，连接，作CH⊥AB交AB的延长线于H，因为A、关于直线EF对称，推出+C=A+C=AC，推出当点P与重合时，P+PC的值最小，最小值=AC的长.
（1）如图1，连接AC，AC交EF于O，
∵四边形ABCD是矩形，
∴AD∥BC，
∴∠OAE=∠OCF，
在△OAE和△OCF中，
，
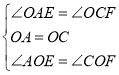∴△OAE≌△OCF，
∴AE=CF，
∵AE∥CF，
∴四边形AFCE是平行四边形，
由翻折得AF=CF，
∴四边形AFCE是菱形；
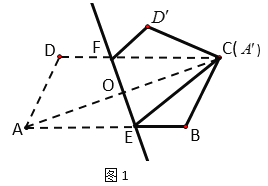
（2）①如图2，作H⊥AB交AB的延长线于H，
在Rt△GBH中，GB=
2，∠GBH=60°，
∴BH=
,GH=
，
设AE=EG=x，
在Rt△EGH中，，
∴
，
解得x=，
∴AE=；
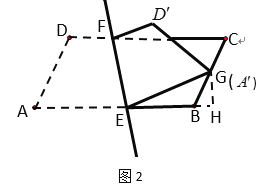
②如图3，连接AC交EF于，连接，作CH⊥AB交AB的延长线于H，
∵A、关于直线EF对称，
∴=A，
∴+C=A+C=AC，
当点P与重合时，P+PC的值最小，最小值=AC的长，
在Rt△BCH中，BC=4，∠CBH=60°，
∴BH=2，CH=
，
∴AH=10，
在Rt△ACH中，AC=
，
∴P+PC的最小值为img src="https://thumb.zyjl.cn/questionBank/Upload/2020/07/22/03/1523d778/SYS202007220311032411941781_DA/SYS202007220311032411941781_DA.002.png" width="33" height="24" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />,
故答案为：.
