题目内容
1. 如图,要建一个面积为150㎡的长方形养鸡场,为了节约材料,鸡场的一边靠着原有的一边墙,墙长为18m,另三边用篱笆围成.若篱笆长度为35m,且要求用完.问:
如图,要建一个面积为150㎡的长方形养鸡场,为了节约材料,鸡场的一边靠着原有的一边墙,墙长为18m,另三边用篱笆围成.若篱笆长度为35m,且要求用完.问:(1)求鸡场的长和宽各为多少米?
(2)若将题中条件“墙长为18米”换为“墙长为a米”,且增加条件“离墙9m开外鸡场一侧准备修条小路”,其他条件不变,则墙长a米至少要多少米?
分析 (1)设鸡场的宽为x米,平行于墙的边长为35-2x米,根据面积为150平方米,可列方程求解.
(2)如果离墙9米开外准备修路,那么宽就要小于9米,可选定墙长为9米,由此进一步分析得出答案即可.
解答 解:(1)设养鸡场靠墙的边长为x米,则平行于墙的边长为(35-2x)米,
由题意得:(35-2x)x=150,
即(2x-15)(x-10)=0,
解得:x=7.5或x=10,
当x=10时,35-2x=15<18,符合实际意义;
当x=7.5时,35-2x=20>18,不符合实际意义,舍去.
答:养鸡场的长是15米,宽是10米;
(2))求出的平行于墙的一条边应小于墙长a;
如果a大于等于20,则方程有两个解,如果a小于20,大于等于15,则有一个解,如果a小于15,则无解.
根据离墙9米开外准备修路,那么长不小于20米,
即a≥20米,
此时养鸡场的长至少为20米,宽为7.5米.
点评 本题考查一元二次方程的实际运用,利用长方形的面积得出等量关系建立方程解决问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.在仓库里堆放着若干个相同的正方体货箱,仓库管理员将这堆货箱从三个方向看到的图形画了出来,如图所示,则这堆正方体货箱共有( )
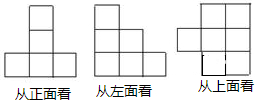

| A. | 9箱 | B. | 10箱 | C. | 11箱 | D. | 12箱 |
 如图,已知BC=DC,需要再添加一个条件∠ACB=∠ACD或AB=AD可得△ABC≌△ADC.
如图,已知BC=DC,需要再添加一个条件∠ACB=∠ACD或AB=AD可得△ABC≌△ADC.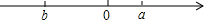 对于有理数a,b,定义一种新运算“⊙”,规定a⊙b=|a+b|+|a-b|.
对于有理数a,b,定义一种新运算“⊙”,规定a⊙b=|a+b|+|a-b|.