题目内容
 在△ABC中,∠A=90°,AB=8,AC=6,M是AB上的动点(不与A,B重合),过M点作MN∥BC交AC于点N.以MN为直径作⊙O,并在⊙O内作内接矩形AMPN.设AM=x.
在△ABC中,∠A=90°,AB=8,AC=6,M是AB上的动点(不与A,B重合),过M点作MN∥BC交AC于点N.以MN为直径作⊙O,并在⊙O内作内接矩形AMPN.设AM=x.
(1)用含x的代数式表示△MNP的面积S;
(2)在动点M的运动过程中,记△MNP与梯形BCNM重合的面积为y,试求y关于x的函数表达式,并求x为何值时,y的值最大,最大值是多少.
解:(1)∵MN∥BC,
∴△AMN∽△ABC,
∴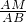 =
=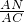 ,即
,即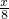 =
= ,解得AN=
,解得AN= x,
x,
∴△AMN的面积= •x•
•x• x=
x= x2,
x2,
∵四边形AMPN是矩形,
∴S= •x•
•x• x=
x= x2(0<x≤8);
x2(0<x≤8);
(2)若P点在BC上时,
∵四边形AMPN是矩形,
∴O点为AP的中点,
而MN∥BC,
∴MN为△ABC的中位线,此时AM=4,
当0<x≤4时,y=S= •x•
•x• x=
x= x2,此时x=4,y的最大值为6;
x2,此时x=4,y的最大值为6;
当4<x≤8时,PM与PN分别交BC于E、F,如图,
y=S梯形MEFN=S△PMN-S△PEF,
∵四边形AMPN是矩形,
∴PN=AM=x,
∵MN∥BC,
∴四边形BFNM是平行四边形,
∴FN=BM=8-x,PF=PN-FN=x-(8-x)=2x-8,
∵Rt△PEF∽Rt△ACB,
∴ =(
=(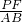 )2=(
)2=( )2,
)2,
而S△ABC= ×8×6=24,
×8×6=24,
∴S△PEF= (x-4)2,
(x-4)2,
∴y= x2-
x2- (x-4)2
(x-4)2
=- x2+12x-24,
x2+12x-24,
=- (x-
(x- )2+8(4<x≤8),
)2+8(4<x≤8),
∵a=- <0,
<0,
∴当x= 时,y有最大值,最大值为8,
时,y有最大值,最大值为8,
综上所述,当x= 时,y有最大值,最大值为8.
时,y有最大值,最大值为8.
分析:(1)先证明△AMN∽△ABC,则可根据相似三角形的对应边成比例求AN,然后由三角形的面积公式求得用x的代数式表示的△AMN的面积S;
(3)先求出P点在BC上时AM的值,然后进行讨论:当0<x≤4时,y=S= •x•
•x• x=
x= x2,根据二次函数的性质得到x=4,y的最大值为6;当4<x≤8时,PM与PN分别交BC于E、F,y=S梯形MEFN=S△PMN-S△PEF,利用矩形的性质可表示出PN=AM=x;再由平行四边形BFNM的性质解得FN=8-x,PF=2x-8,则可利用相似三角形Rt△PEF∽Rt△ABC的性质求得S△PEF值;然后写出y与x的解析式,再根据二次函数的性质求出y的最大值,最后综合两种情况即可.
x2,根据二次函数的性质得到x=4,y的最大值为6;当4<x≤8时,PM与PN分别交BC于E、F,y=S梯形MEFN=S△PMN-S△PEF,利用矩形的性质可表示出PN=AM=x;再由平行四边形BFNM的性质解得FN=8-x,PF=2x-8,则可利用相似三角形Rt△PEF∽Rt△ABC的性质求得S△PEF值;然后写出y与x的解析式,再根据二次函数的性质求出y的最大值,最后综合两种情况即可.
点评:本题考查了圆的综合题:掌握圆周角定理及其推论;熟练运用相似三角形的有关知识进行几何计算和二次函数的性质解决最值问题.

∴△AMN∽△ABC,
∴
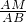 =
=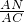 ,即
,即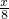 =
= ,解得AN=
,解得AN= x,
x,∴△AMN的面积=
 •x•
•x• x=
x= x2,
x2,∵四边形AMPN是矩形,
∴S=
 •x•
•x• x=
x= x2(0<x≤8);
x2(0<x≤8);(2)若P点在BC上时,
∵四边形AMPN是矩形,
∴O点为AP的中点,
而MN∥BC,
∴MN为△ABC的中位线,此时AM=4,
当0<x≤4时,y=S=
 •x•
•x• x=
x= x2,此时x=4,y的最大值为6;
x2,此时x=4,y的最大值为6;当4<x≤8时,PM与PN分别交BC于E、F,如图,
y=S梯形MEFN=S△PMN-S△PEF,
∵四边形AMPN是矩形,
∴PN=AM=x,
∵MN∥BC,
∴四边形BFNM是平行四边形,
∴FN=BM=8-x,PF=PN-FN=x-(8-x)=2x-8,
∵Rt△PEF∽Rt△ACB,
∴
 =(
=(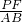 )2=(
)2=( )2,
)2,而S△ABC=
 ×8×6=24,
×8×6=24,∴S△PEF=
 (x-4)2,
(x-4)2,∴y=
 x2-
x2- (x-4)2
(x-4)2=-
 x2+12x-24,
x2+12x-24,=-
 (x-
(x- )2+8(4<x≤8),
)2+8(4<x≤8),∵a=-
 <0,
<0,∴当x=
 时,y有最大值,最大值为8,
时,y有最大值,最大值为8,综上所述,当x=
 时,y有最大值,最大值为8.
时,y有最大值,最大值为8.分析:(1)先证明△AMN∽△ABC,则可根据相似三角形的对应边成比例求AN,然后由三角形的面积公式求得用x的代数式表示的△AMN的面积S;
(3)先求出P点在BC上时AM的值,然后进行讨论:当0<x≤4时,y=S=
 •x•
•x• x=
x= x2,根据二次函数的性质得到x=4,y的最大值为6;当4<x≤8时,PM与PN分别交BC于E、F,y=S梯形MEFN=S△PMN-S△PEF,利用矩形的性质可表示出PN=AM=x;再由平行四边形BFNM的性质解得FN=8-x,PF=2x-8,则可利用相似三角形Rt△PEF∽Rt△ABC的性质求得S△PEF值;然后写出y与x的解析式,再根据二次函数的性质求出y的最大值,最后综合两种情况即可.
x2,根据二次函数的性质得到x=4,y的最大值为6;当4<x≤8时,PM与PN分别交BC于E、F,y=S梯形MEFN=S△PMN-S△PEF,利用矩形的性质可表示出PN=AM=x;再由平行四边形BFNM的性质解得FN=8-x,PF=2x-8,则可利用相似三角形Rt△PEF∽Rt△ABC的性质求得S△PEF值;然后写出y与x的解析式,再根据二次函数的性质求出y的最大值,最后综合两种情况即可.点评:本题考查了圆的综合题:掌握圆周角定理及其推论;熟练运用相似三角形的有关知识进行几何计算和二次函数的性质解决最值问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在△ABC中,∠C=90°,BC=12,AB=13,则tanA的值是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
在△ABC中,a=
,b=
,c=2
,则最大边上的中线长为( )
| 2 |
| 6 |
| 2 |
A、
| ||
B、
| ||
| C、2 | ||
| D、以上都不对 |
 23、如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.
23、如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.
 18、如图,在△ABC中,边AC的垂直平分线交BC于点D,交AC于点E、已知△ABC中与△ABD的周长分别为18cm和12cm,则线段AE的长等于
18、如图,在△ABC中,边AC的垂直平分线交BC于点D,交AC于点E、已知△ABC中与△ABD的周长分别为18cm和12cm,则线段AE的长等于