题目内容
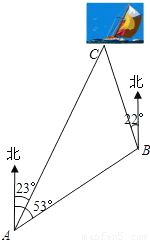
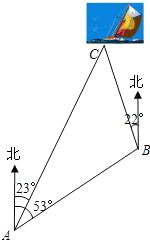 一艘小船从码头A出发,沿北偏东53°方向航行,航行一段时间到达小岛B处后,又沿着北偏西22°方向航行了10海里到达C处,这时从码头测得小船在码头北偏东23°的方向上,求此时小船与码头之间的距离(
一艘小船从码头A出发,沿北偏东53°方向航行,航行一段时间到达小岛B处后,又沿着北偏西22°方向航行了10海里到达C处,这时从码头测得小船在码头北偏东23°的方向上,求此时小船与码头之间的距离(| 2 |
| 3 |
分析:根据题意知:在△ABC中,∠BAC=30°,∠C=45°,BC=10海里,求AC长,解斜三角形ABC需转化为解直角三角形求解,因此需作高,作BD⊥AC于D点,分别求AD和CD长.
解答: 解:∵∠BAC=53°-23°=30°,
解:∵∠BAC=53°-23°=30°,
∴∠C=23°+22°=45°.
过点B作BD⊥AC,垂足为D,则CD=BD.
∵BC=10,
∴CD=BC•cos45°=10×
=5
≈7.0,
∴AD=
=5
÷
=5
×
=5
×
≈5×1.4×1.7≈11.9.
∴AC=AD+CD=11.9+7.0=18.9≈19.
答:小船到码头的距离约为19海里.
 解:∵∠BAC=53°-23°=30°,
解:∵∠BAC=53°-23°=30°,∴∠C=23°+22°=45°.
过点B作BD⊥AC,垂足为D,则CD=BD.
∵BC=10,
∴CD=BC•cos45°=10×
| ||
| 2 |
| 2 |
∴AD=
| BD |
| tan30° |
| 2 |
| ||
| 3 |
| 2 |
| 3 | ||
|
| 2 |
| 3 |
∴AC=AD+CD=11.9+7.0=18.9≈19.
答:小船到码头的距离约为19海里.
点评:“化斜为直”是解三角形的基本思路,常需作垂线(高),原则上不破坏特殊角(30°、45°、60°).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
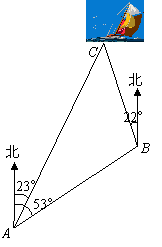
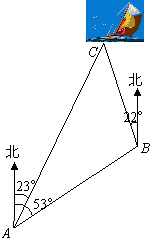
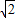 ≈1.4,
≈1.4,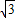 ≈1.7,结果保留整数).
≈1.7,结果保留整数).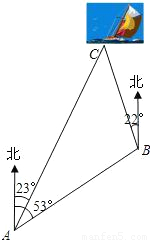
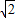 ≈1.4,
≈1.4,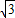 ≈1.7,结果保留整数).
≈1.7,结果保留整数).