题目内容
 已知,如图,AD是△ABC的角平分线,DE∥AC,ED=AF.求证:四边形AEDF是菱形.
已知,如图,AD是△ABC的角平分线,DE∥AC,ED=AF.求证:四边形AEDF是菱形.
证明:∵AD是△ABC的角平分线
∴∠EAD=∠FAD
∵DE∥AC,ED=AF
∴四边形AEDF是平行四边形
∴∠EAD=∠ADF
∴∠FAD=∠FDA
∴AF=DF
∴四边形AEDF是菱形.
分析:由已知易得四边形AEDF是平行四边形,由角平分线和平行线的定义可得∠FAD=∠FDA,则可求得AF=DF,故可证明四边形AEDF是菱形.
点评:此题主要考查菱形的判定、角平分线的定义和平行线的性质.此题运用了菱形的判定方法“一组邻边相等的平行四边形是菱形”.
∴∠EAD=∠FAD
∵DE∥AC,ED=AF
∴四边形AEDF是平行四边形
∴∠EAD=∠ADF
∴∠FAD=∠FDA
∴AF=DF
∴四边形AEDF是菱形.
分析:由已知易得四边形AEDF是平行四边形,由角平分线和平行线的定义可得∠FAD=∠FDA,则可求得AF=DF,故可证明四边形AEDF是菱形.
点评:此题主要考查菱形的判定、角平分线的定义和平行线的性质.此题运用了菱形的判定方法“一组邻边相等的平行四边形是菱形”.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
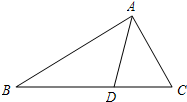 已知:如图,AD是△ABC的角平分线,且AB:AC=3:2,则△ABD与△ACD的面积之比为( )
已知:如图,AD是△ABC的角平分线,且AB:AC=3:2,则△ABD与△ACD的面积之比为( )| A、3:2 | B、9:4 | C、2:3 | D、4:9 |
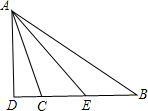 已知:如图,AD是△ABC的高,试判断∠DAE与∠B、∠ACB之间的关系,并说明理由.
已知:如图,AD是△ABC的高,试判断∠DAE与∠B、∠ACB之间的关系,并说明理由.
 已知:如图,AD是一条直线,∠1=65°,∠2=115°.求证:BE∥CF.
已知:如图,AD是一条直线,∠1=65°,∠2=115°.求证:BE∥CF. 已知:如图,AD是△ABC的平分线,点E在BC上,点G在CA的延长线上,EG交AB于点F,且∠AFG=∠G.求证:GE∥AD.
已知:如图,AD是△ABC的平分线,点E在BC上,点G在CA的延长线上,EG交AB于点F,且∠AFG=∠G.求证:GE∥AD.