Question

【题目】抛物线 y＝ax2＋bx＋3 经过点(2，－1)，与 x 轴交于 A(1，0)、B 两点，与 y轴交于点 C

(1) 求抛物线解析式

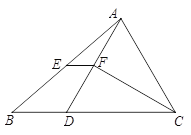
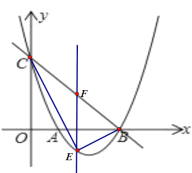
(2) 如图，点 E 是直线 BC 下方抛物线上的一动点．当△BEC 面积最大时，请求出点 E 的坐标

(3) 点 P 是第四象限内抛物线上的一动点，PA 交 y 轴于 D，BP 交 y 轴于 E，过 P 作 PN⊥y 轴于N，求的值

Answer 1

【答案】(1) y＝x2-4x＋3；(2) E(，)； (3).

【解析】

(1) 将点(2，－1)和点A(1，0)代入抛物线，解出a，b的值，即可得到解析式；

(2) 求出B、C坐标和直线BC的解析式，设E(x，x-4x+3)，作EF垂直于x轴于BC交于F点，可得F(x，-x+3)，将△BEC分为△BEF和△CEF，列出式子解得x，即可求得E的坐标；

(3)设P(，)，求出直线PA、PB的解析式，算出D、E的坐标，可得到DE=，又因为PN=，可求.

(1)将点(2，－1)和点A(1，0)代入抛物线，得

，

解得，，

∴抛物线解析式为y＝x2-4x＋3；

(2)由抛物线y＝x2-4x＋3得B(1，0)，C(0，3)，

解得直线BC的解析式为，BC=，

设E(x，x-4x+3)，

作EF垂直于x轴于BC交于F点，可得F(x，-x+3)，

则

，

当，即E(，)时，△BEC 面积最大；

(3)

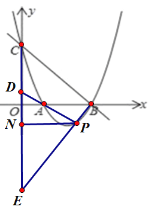
设P(，)，

可求得直线PB：，

直线PA：，

∴D(0,),E(0,),

DE=-=,

由图知PN=，

∴.