题目内容
如图,△ABC为等腰三角形,AB=AC,O是底边BC的中点,⊙O与腰AB相切于点D,
求证:AC与⊙O相切。

连结OD,过点O作OE⊥AC于E点,先根据切线的性质可得OD⊥AB,即可得∠ODB=∠OEC=90°,再结合O是底边BC的中点根据等腰三角形的性质可得OB=OC,再由AB=AC可得∠B=∠C,即可证得△OBE≌△OCE,从而得到结论.
解析试题分析:连结OD,过点O作OE⊥AC于E点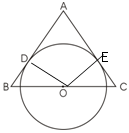
∵AB切⊙O于D,
∴OD⊥AB.
∴∠ODB=∠OEC=90°.
又∵O是BC的中点,
∴OB=OC.
∵AB=AC,
∴∠B=∠C.
∴△OBE≌△OCE.
∴OE=OD,即OE是⊙O的半径.
∴AC与⊙O相切.
考点:切线的性质,等腰三角形的性质,全等三角形的判定和性质
点评:本题知识点较多,综合性较强,是中考常见题,难度不大,正确作出辅助线是解题的关键.

练习册系列答案
相关题目
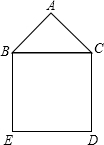 如图,△ABC为等腰直角三角形,它的面积为8平方厘米,以它的斜边为边的正方形BCDE的面积为( )平方厘米.
如图,△ABC为等腰直角三角形,它的面积为8平方厘米,以它的斜边为边的正方形BCDE的面积为( )平方厘米.| A、16 | B、24 | C、64 | D、32 |
 2、如图,△ABC为等腰三角形,AB=AC,∠A=40°,D,E,F分别在BC,AC,AB上,且CE=CD,BD=BF,则∠EDF的度数为( )
2、如图,△ABC为等腰三角形,AB=AC,∠A=40°,D,E,F分别在BC,AC,AB上,且CE=CD,BD=BF,则∠EDF的度数为( ) 如图,△ABC为等腰直角三角形∠BAC=90°,AD是斜边BC上的中线,△ABD旋转到△ACE的位置.
如图,△ABC为等腰直角三角形∠BAC=90°,AD是斜边BC上的中线,△ABD旋转到△ACE的位置. (2013•六合区一模)如图,△ABC为等腰直角三角形,∠C=90°,若在某一平面直角坐标系中,顶点C的坐标为(1,1),B的坐标为(2,0).则顶点A的坐标是( )
(2013•六合区一模)如图,△ABC为等腰直角三角形,∠C=90°,若在某一平面直角坐标系中,顶点C的坐标为(1,1),B的坐标为(2,0).则顶点A的坐标是( ) 如图,△ABC为等腰三角形,如果把它沿底边BC翻折后,得到△DBC,那么四边形ABDC为( )
如图,△ABC为等腰三角形,如果把它沿底边BC翻折后,得到△DBC,那么四边形ABDC为( )