题目内容
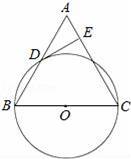
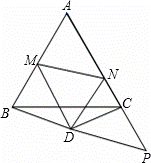
如图,已知△ABC中,AB=AC=1,∠ABC=∠ACB=60°,点D是△ABC外一点,且BD=DC,∠DBC=∠DCB=30°,又点M、N分别在AB、AC上,∠MDN=60°,小明为探求△AMN的周长,在AC的延长线上截取了CP=BM,并连接DP,
(1)试说明:MN=NP;
(2)求出△AMN的周长.
略;2.
详解:(1)∵∠ABC=∠ACB=60°,∠DBC=∠DCB=30°,
∴∠ABD=∠ACD=90°,
在△MBD和△PCD中,MB=PC,∠ABD=∠ACD,BD=CD,
∴△MBD≌△PCD(SAS),
∴MD=PD,∠MDB=∠PDC,
又∵∠DBC=∠DCB=30°,∴∠BDC=120°,
∴∠MDB+∠MDC=120°,
∴∠PDC+∠MDC=120°,即∠PDM=120°,
又∵∠MDN=60°,∴∠PDN=60°,
∴∠MDN=∠PDN=60°,
在△MDN和△PDN中,MD=PD,∠MDN=∠PDN,DN=DN,
∴△MDN≌△PDN(SAS),∴MN=NP;
(2)△AMN的周长:
AM+MN+AN=AM+NP+AN=AM+AP=AM+AC+CP=AM+AC+BM=AB+AC=1+1=2;
∴△AMN的周长为2.

练习册系列答案
相关题目
 的解为
的解为 ,则
,则
 中,点
中,点 是
是 的中点,过点
的中点,过点 ,
, 的延长线于点
的延长线于点 ,
, . 当
. 当 时,求证:
时,求证: .
.
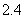 B. 4 C.
B. 4 C. 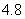 D. 5
D. 5
 A. B. C. D.
A. B. C. D.  形,使其为轴对称图形.(要求:分别在图①、图②、图③中画出三个互不相同的图形)
形,使其为轴对称图形.(要求:分别在图①、图②、图③中画出三个互不相同的图形)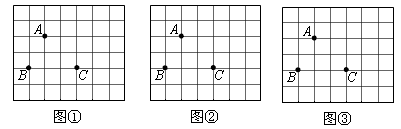
 的整数部分,
的整数部分, ,则(2a+1)2的平方根是_______________.
,则(2a+1)2的平方根是_______________.
 ,求DE的长.
,求DE的长.