题目内容
已知抛物线C1与x轴的一个交点为交于(-4,0),对称轴为直线x=-1.5,
并过点(-1,6)
1.求抛物线C1的解析式;
2.求出与抛物线C1关于原点对称的抛物线C2的解析式,并在C1所在的平面直角坐标系中画出C2的图像;
3.在(2)的条件下,抛物线C1 与抛物线C2与相交于A,B两点(点A在点B的左侧).
①求出点A和点B的坐标;
②点P在抛物线![]() 上,且位于点A和点B之间;点Q在抛物线
上,且位于点A和点B之间;点Q在抛物线![]() 上,也位于点A和点B之间.当PQ∥
上,也位于点A和点B之间.当PQ∥![]() 轴时,求PQ长度的最大值.
轴时,求PQ长度的最大值.

1.C1:![]()
2.![]() :
:![]()
3.①A (-2,6);B (2,-6)②PQ的最大值为8
解析:⑴ C1:![]() ……2分
……2分
⑵ ![]() :
:![]() ……4分
……4分
其图像如图所示 ……5分
⑶ ①A (-2,6);B (2,-6) ……7分
② 设P(a,b),则-2≤a≤2,![]() ,
,
因为PQ∥y轴,所以点Q的横坐标为a,则![]() ,
,
所以PQ=![]() =
=![]() , ……9分
, ……9分
即当a=0时,PQ的最大值为8


练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
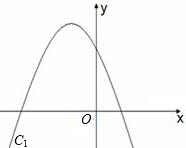 已知抛物线C1与x轴的一个交点为交于(-4,0),对称轴为x=-1.5,并过点(-1,6),
已知抛物线C1与x轴的一个交点为交于(-4,0),对称轴为x=-1.5,并过点(-1,6), (2013•燕山区一模)己知二次函数
(2013•燕山区一模)己知二次函数 上,且位于点A和点B之间;点Q在抛物线
上,且位于点A和点B之间;点Q在抛物线 上,也位于点A和点B之间.当PQ∥
上,也位于点A和点B之间.当PQ∥ 轴时,求PQ长度的最大值.
轴时,求PQ长度的最大值.

