题目内容
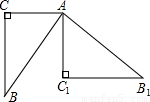
如图，桌面上放着一块三角板ABC，其中∠C=90°，AC=8，BC=14，把三角板绕顶点A顺时针旋转90°，原三角板旋转到△AB1C1的位置，那么sin∠CBC1的值为分析：根据题意作图，可根据图示得出□ACDC1及RT△BC1D，然后根据勾股定理及锐角三角函数定义得出结果．
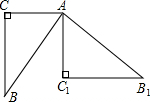
解答：
解：连接BC1，过C1做BC的垂线角BC于点D，如图：
根据图示得出?ACDC1，
∵DC1=AC=8，BD=BC-AC1=14-8=6，
在RT△BC1D中，根据勾股定理得：
BC1=
=10，
∴sin∠CBC1=
=
=
．
故答案为：
．
解：连接BC1，过C1做BC的垂线角BC于点D，如图：根据图示得出?ACDC1，
∵DC1=AC=8，BD=BC-AC1=14-8=6，
在RT△BC1D中，根据勾股定理得：
BC1=
| BD2+ C1D2 |
∴sin∠CBC1=
| DC1 |
| BC1 |
| 8 |
| 10 |
| 4 |
| 5 |
故答案为：
| 4 |
| 5 |
点评：本题主要考查了正方形、直角三角形勾股定理以及锐角三角函数，难度适中．
练习册系列答案
相关题目
如图，桌面上放着一块三角板ABC，其中∠C=90°，AC=8，BC=14，把三角板绕顶点A顺时针旋转90°，原三角板旋转到△AB1C1的位置，那么sin∠CBC1的值为________．