题目内容
朝晖初中的科技活动搞得有声有色.某班的小赵对跨湖桥博物馆富有创意的独木舟形象设计很有兴趣,他回家后将一正五边形纸片沿其对称轴对折.旋转放置,做成独木舟模型.如图所示,该正五边形ABCDE中,O为中心,延长AO交CD于点M.若OM长为
,AN为独木舟船头A到船底的距离,为了计算AN+
AM的值,小赵所在的科技小组进行了热烈的讨论:
小王:AM显然是此正五边形的对称轴.
小李:AN与AM似乎无法直接求出,应该用整体思想来求AN+
AM的值.
小朱:注意到AM⊥CM,AN⊥BC,则AM与AN可看成是三角形的高,能否利用面积法来求呢?
小杨:若将点O与正五边形的各顶点连接,则将此正五边形的面积五等分…

在这些同学的提示下,小赵求出了AN+
AM=______.
| 6 |
| 1 |
| 2 |
小王:AM显然是此正五边形的对称轴.
小李:AN与AM似乎无法直接求出,应该用整体思想来求AN+
| 1 |
| 2 |
小朱:注意到AM⊥CM,AN⊥BC,则AM与AN可看成是三角形的高,能否利用面积法来求呢?
小杨:若将点O与正五边形的各顶点连接,则将此正五边形的面积五等分…

在这些同学的提示下,小赵求出了AN+
| 1 |
| 2 |

设正五边形的边长是x,则五边形的面积是
| 1 |
| 2 |
5
| ||
| 2 |
5
| ||
| 4 |
而ABCM的面积=△ACM得面积+△ACB的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| AM |
| 4 |
| 1 |
| 2 |
则
| AM |
| 4 |
| 1 |
| 2 |
5
| ||
| 4 |
则:AN+
| 1 |
| 2 |
| 5 |
| 2 |
| 6 |

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目

 ,AN为独木舟船头A到船底的距离,为了计算
,AN为独木舟船头A到船底的距离,为了计算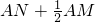 的值,小赵所在的科技小组进行了热烈的讨论:
的值,小赵所在的科技小组进行了热烈的讨论: