Question

【题目】如图，在平面直角坐标系中，已知矩形ABCD的三个顶点B（1, 0）、C（3, 0）、D（3, 4）．以A为顶点的抛物线y＝ax2＋bx＋c过点C．动点P从点A出发，以每秒个单位的速度沿线段AD向点D运动，运动时间为t秒．过点P作PE⊥x轴交抛物线于点M，交AC于点N．

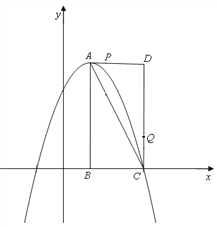
（1）直接写出点A的坐标，并求出抛物线的解析式；

（2）当t为何值时，△ACM的面积最大？最大值为多少？

（3）点Q从点C出发，以每秒1个单位的速度沿线段CD向点D运动，当t为何值时，在线段PE上存在点H，使以C、Q、N、H为顶点的四边形为菱形？

Answer 1

【答案】（1）A（1，4）；y＝－x2＋2x＋3；（2）当t＝２时，△AＭC面积的最大值为1；（3）或．

【解析】（1）由矩形的性质得到点A的坐标，由抛物线的顶点为A，设抛物线的解析式为y＝a（x－1）2＋4，把点C的坐标代入即可求得a的值；

（2）由点P的坐标以及抛物线解析式得到点M的坐标，由A、C的坐标得到直线AC的解析式，进而得到点N的坐标，即可用关于t的式子表示MN，然后根据△ACM的面积是△AMN和△CMN的面积和列出用t表示的△ACM的面积，利用二次函数的性质即可得到当t＝２时，△AＭC面积的最大值为1；

（3）①当点Ｈ在Ｎ点上方时，由PＮ＝CQ，PN∥CQ，得到四边形PNCQ为平行四边形，所以当PQ＝CQ时，四边形FECQ为菱形，据此得到，解得t值；②当点Ｈ在Ｎ点下方时，NH=CQ=，NQ＝CQ时，四边形NHCQ为菱形，NQ2＝CQ2，得：，解得t值．

解：（1）由矩形的性质可得点A（1，4），

∵抛物线的顶点为A，

设抛物线的解析式为y＝a（x－1）2＋4，

代入点C（3, 0），可得a＝－1．

∴y＝－（x－1）2＋4＝－x2＋2x＋3．

（2）∵P（，４），

将代入抛物线的解析式，y＝－（x－1）2＋4＝，

∴M（， ），

设直线AC的解析式为，

将A（１,４），C（３,０）代入，得：，

将代入得，

∴N（，），

∴MN ，

∴，

∴当t＝２时，△AＭC面积的最大值为1．

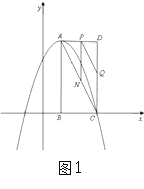
（3）①如图１，当点Ｈ在Ｎ点上方时，

∵Ｎ（，），P（，４），

∴PＮ＝４—（）＝＝CQ，

又∵PN∥CQ，

∴四边形PNCQ为平行四边形，

∴当PQ＝CQ时，四边形FECQ为菱形，

PQ2＝PD2+DQ2 ＝，

∴，

整理，得．解得， （舍去）；

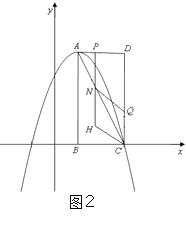
②如图２当点Ｈ在Ｎ点下方时，

NH=CQ=，NQ＝CQ时，四边形NHCQ为菱形，

NQ2＝CQ2，得：．

整理，得． ．所以，（舍去）．

“点睛”此题主要考查二次函数的综合问题，会用顶点式求抛物线，会用两点法求直线解析式，会设点并表示三角形的面积，熟悉矩形和菱形的性质是解题的关键.