题目内容
如图,四边形ABCD的对角线AC,BD相交于点O, 。
。
求证:AB∥CD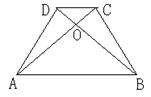
 。
。求证:AB∥CD

∵
∴AD=BC,∠ADB=∠ACB
∵∠AOD=∠BOC
∴△ADO≌△BCO
∴AO=BO,CO=DO
∴∠OAB=∠OBA, ∠ODC=∠OCD
∴∠OAB=∠OCD
∴AB∥CD

∴AD=BC,∠ADB=∠ACB
∵∠AOD=∠BOC
∴△ADO≌△BCO
∴AO=BO,CO=DO
∴∠OAB=∠OBA, ∠ODC=∠OCD
∴∠OAB=∠OCD
∴AB∥CD
先证出△ADO≌△BCO,然后得出△ABO与△CDO是等腰三角形,得出∠OAB=∠OCD,从而证出AB∥CD.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目



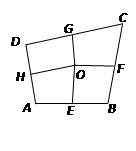
 ;
;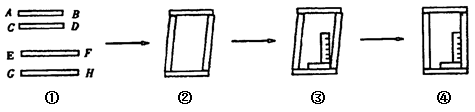

 时,t是多少?
时,t是多少?