Question

【题目】二次函数

（1）画出上述二次函数的图象；

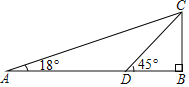
（2）如图，二次函数的图象与x轴的其中一个交点是B，与y轴的交点是C，直线BC与反比例函数的图象交于点D，且BC=3CD，求反比例函数的解析式.

（3）在（2）的条件下，x轴上的点P的横坐标是多少时，△BCP与△OCD相似.

Answer 1

【答案】（1）见解析；（2）；（3）P的横坐标为5或12时，ΔBCP∽ΔOCD.

【解析】

（1）列表，分别取x值代入解析式得出y值，建立坐标系描点，用平滑的曲线连线即可；（2）由（1）可得B、C两点的坐标，过D作DE⊥y轴于E，可证明ΔDEC∽ΔBOC，根据相似三角形的性质可得，由BC=3CD可求出DE=CE=1，即可求出D点坐标，设反比例函数解析式为y=，把D点坐标代入求出k值即可得答案；（3）由，分别讨论和两种情况，求出BP的长即可.

（1）①列表

x	…	-1	0	1	2	3	…
	…	0	-3	-4	-3	0	…

②描点；

③连线，

二次函数图象如图所示：

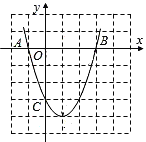
（2）由（1）可知B（3，0）、C（0，-3）

∴OB=OC=3

过D作DE⊥y轴于E

∵∠DCE=∠OCB，∠BOC=∠DEC=90°，

∴ΔDEC∽ΔBOC.

∴

∵BC=3CD

∴DE=CE=1

∴OE=4

∴D（-1，-4）

设反比例函数为，

∴，即k=4.

∴反比例函数为.

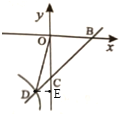
（3）

情况1.

∴，即BP=9

∴P(12，0)

情况2.当

∴，即BP=2

∴P(5，0)

综合以上两种情况，当P的横坐标为5或12时，ΔBCP∽ΔOCD