题目内容
(2013•西城区一模)已知关于x的一元二次方程2x2+(a+4)x+a=0.
(1)求证:无论a为任何实数,此方程总有两个不相等的实数根;
(2)抛物线C1:y=2x2+(a+4)x+a与x轴的一个交点的横坐标为
,其中a≠0,将抛物线C1向右平移
个单位,再向上平移
个单位,得到抛物线C2.求抛物线C2的解析式;
(3)点A(m,n)和B(n,m)都在(2)中抛物线C2上,且A、B两点不重合,求代数式2m3-2mn+2n3的值.
(1)求证:无论a为任何实数,此方程总有两个不相等的实数根;
(2)抛物线C1:y=2x2+(a+4)x+a与x轴的一个交点的横坐标为
| a |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
(3)点A(m,n)和B(n,m)都在(2)中抛物线C2上,且A、B两点不重合,求代数式2m3-2mn+2n3的值.
分析:(1)先求出判别式的值,根据△>0时,方程有两个不相等的实数根,即可得出结论;
(2)将点(
,0)代入抛物线C1解析式,得出a的值,从而确定C1解析式,根据平移的规律可得出抛物线C2的解析式;
(3)将点A(m,n)和B(n,m)代入抛物线C2的解析式,通过整理、化简可得出代数式2m3-2mn+2n3的值.
(2)将点(
| a |
| 2 |
(3)将点A(m,n)和B(n,m)代入抛物线C2的解析式,通过整理、化简可得出代数式2m3-2mn+2n3的值.
解答:(1)证明:∵△=(a+4)2-4×2a=a2+16,
而a2≥0,
∴a2+16>0,即△>0.
∴无论a为任何实数,此方程总有两个不相等的实数根.
(2)∵当x=
时,y=0,
∴2×(
)2+(a+4)×
+a=0,
∴a2+3a=0,即a(a+3)=0,
∵a≠0,
∴a=-3.
∴抛物线C1的解析式为y=2x2+x-3=2(x+
)2-
,
∴抛物线C1的顶点为(-
,-
),
∴抛物线C2的顶点为(0,-3).
∴抛物线C2的解析式为y=2x2-3.
(3)∵点A(m,n)和B(n,m)都在抛物线C2上,
∴n=2m2-3,m=2n2-3,
∴n-m=2(m2-n2),
∴n-m=2(m-n)(m+n),
∴(m-n)[2(m+n)+1]=0,
∵A、B两点不重合,即m≠n,
∴2(m+n)+1=0,
∴m+n=-
,
∵2m2=n+3,2n2=m+3,
∴2m3-2mn+2n3=2m2•m-2mn+2n2•n=(n+3)•m-2mn+(m+3)•n=3(m+n)=-
.
而a2≥0,
∴a2+16>0,即△>0.
∴无论a为任何实数,此方程总有两个不相等的实数根.
(2)∵当x=
| a |
| 2 |
∴2×(
| a |
| 2 |
| a |
| 2 |
∴a2+3a=0,即a(a+3)=0,
∵a≠0,
∴a=-3.
∴抛物线C1的解析式为y=2x2+x-3=2(x+
| 1 |
| 4 |
| 25 |
| 8 |
∴抛物线C1的顶点为(-
| 1 |
| 4 |
| 25 |
| 8 |
∴抛物线C2的顶点为(0,-3).
∴抛物线C2的解析式为y=2x2-3.
(3)∵点A(m,n)和B(n,m)都在抛物线C2上,
∴n=2m2-3,m=2n2-3,
∴n-m=2(m2-n2),
∴n-m=2(m-n)(m+n),
∴(m-n)[2(m+n)+1]=0,
∵A、B两点不重合,即m≠n,
∴2(m+n)+1=0,
∴m+n=-
| 1 |
| 2 |
∵2m2=n+3,2n2=m+3,
∴2m3-2mn+2n3=2m2•m-2mn+2n2•n=(n+3)•m-2mn+(m+3)•n=3(m+n)=-
| 3 |
| 2 |
点评:本题考查了二次函数的综合题,涉及了根的判别式、二次函数的几何变换及代数式求值的知识,同学们需要注意培养自己解决综合题的能力,第三问需要我们灵活变换才能得出答案.

练习册系列答案
相关题目
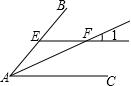 (2013•西城区一模)如图,AF是∠BAC的平分线,EF∥AC交AB于点E.若∠1=25°,则∠BAF的度数为( )
(2013•西城区一模)如图,AF是∠BAC的平分线,EF∥AC交AB于点E.若∠1=25°,则∠BAF的度数为( ) (2013•西城区一模)如图,在矩形ABCD中,AB=2,BC=4.将矩形ABCD绕点C沿顺时针方向旋转90°后,得到矩形FGCE(点A、B、D的对应点分别为点F、G、E).动点P从点B开始沿BC-CE运动到点E后停止,动点Q从点E开始沿EF-FG运动到点G后停止,这两点的运动速度均为每秒1个单位.若点P和点Q同时开始运动,运动时间为x(秒),△APQ的面积为y,则能够正确反映y与x之间的函数关系的图象大致是( )
(2013•西城区一模)如图,在矩形ABCD中,AB=2,BC=4.将矩形ABCD绕点C沿顺时针方向旋转90°后,得到矩形FGCE(点A、B、D的对应点分别为点F、G、E).动点P从点B开始沿BC-CE运动到点E后停止,动点Q从点E开始沿EF-FG运动到点G后停止,这两点的运动速度均为每秒1个单位.若点P和点Q同时开始运动,运动时间为x(秒),△APQ的面积为y,则能够正确反映y与x之间的函数关系的图象大致是( )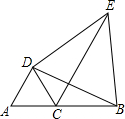 (2013•西城区一模)如图,点C在线段AB上,△DAC和△DBE都是等边三角形.
(2013•西城区一模)如图,点C在线段AB上,△DAC和△DBE都是等边三角形.