题目内容
我们知道海拔一定高度的山区气温随着海拔高度的增加而下降．小明暑假到黄山去旅游，沿途他利用随身所带的测量仪器，测得以下数据：
| 海拔高度x（m） | 1400 | 1500 | 1600 | 1700 | … |
| 气温y（°C） | 32.00 | 31.40 | 30.80 | 30.20 | … |
（2）已知y与x的关系是一次函数关系，求出这个关系式；
（3）若小明到达黄山天都峰时测得当时的气温是29.24°C．求黄山天都峰的海拔高度．
解：（1）描点：
（2）设解析式为y=kx+b，把点（1400，32），（1500，31.4）分别代入可得：
，
解得：
，
所以此一次函数关系式为：y=-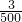
x+40.4；
（3）当y=29.24时，有：
x+40.4=29.24，
解得：x=
，
即山巅的海拔为：米．
分析：（1）利用描点法找到表格中的对应点；
（2）设解析式为y=kx+b，把点（1400，32），（1500，31.4）分别代入，利用待定系数法可求得；
（3）气温为29.24℃，求这里的海拔高度，其实就是求当y=29.24时x的值，解方程即可．
点评：此题考查了一次函数的应用以及利用一次函数的模型解决实际问题的能力．要先根据题意列出函数关系式，再代数求值．解题的关键是要分析题意根据实际意义准确的列出解析式，再把对应值代入求解．
（2）设解析式为y=kx+b，把点（1400，32），（1500，31.4）分别代入可得：
，解得：
，所以此一次函数关系式为：y=-
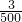x+40.4；（3）当y=29.24时，有：
x+40.4=29.24，解得：x=
，即山巅的海拔为：
米．分析：（1）利用描点法找到表格中的对应点；
（2）设解析式为y=kx+b，把点（1400，32），（1500，31.4）分别代入，利用待定系数法可求得；
（3）气温为29.24℃，求这里的海拔高度，其实就是求当y=29.24时x的值，解方程即可．
点评：此题考查了一次函数的应用以及利用一次函数的模型解决实际问题的能力．要先根据题意列出函数关系式，再代数求值．解题的关键是要分析题意根据实际意义准确的列出解析式，再把对应值代入求解．
练习册系列答案
相关题目