题目内容
如图，点G是正方形ABCD对角线CA的延长线上任意一点，以线段AG为边作一个正方形AEFG，线段EB和GD相交于点H．若AB=
，AG=1，则EB= ．
∵四边形ABCD、AGFE是正方形，
∴AB=AD，AE=AG，∠DAB=∠EAG，
∴∠EAB=∠GAD，
在△AEB和△AGD中，
，
∴△EAB≌△GAD（SAS），
∴EB=GD，
∵四边形ABCD是正方形，AB=，
∴BD⊥AC，AC=BD=
AB=2，
∴∠DOG=90°，OA=OD=
BD=1，
∵AG=1，
∴OG=OA+AG=2，
∴GD=
=
，
∴EB=．
故答案为：．
练习册系列答案
相关题目
反比例函数y1=
和正比例函数y2=mx的图象如图，根据图象可以得到满足y1＜y2的x的取值范围是（ ）
|
|
A． | x＞1 | B． | ﹣＜x＜1或x＜﹣1 | C． | ﹣1＜x＜0或x＞1 | D． | x＞2或x＜1 |
2014年西宁市教育局建立了“西宁招考信息网”，实现了“网上二填报三公开三查询”，标志着西宁中考迈出网络化管理第一步，在全市第二次模拟考试实战演练后，通过网上查询，某校数学教师对本班数学成绩（成绩取整数，满分为120分）作了统计分析，绘制成频数分布步和频数分布直方图，请你根据图表提供的信息，解答下列问题：
频数分布表：
| 分组 | 频数 | 频率 |
| 60＜x≤72 | 2 | 0.04 |
| 72＜≤84 | 8 | 0.16 |
| 84＜x≤96 | 20 | a |
| 96＜x≤108 | 16 | 0.32 |
| 108＜x≤120 | b | 0.08 |
| 合计 | 50 | 1 |
（1）频数分布表中a= ，b= ；
（2）补全频数分布直方图；
（3）为了激励学生，教师准备从超过108分的学生中选2人介绍学习经验，那么取得118分的小红和112分的小明同时被选上的概率是多少？请用列表法或画树形图加以说明，并列出所有可能的结果．
∥
，
与
相交于点
， 
，
，则
的度数为（ ）
Ｂ．
Ｃ．
Ｄ．
品牌的文具盒40个，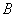
品牌的文具盒60个．其中
= , 
= , 
= , 
= .