题目内容
【题目】如图,四边形ABCD,AD∥BC,∠B=90°,AD=6,AB=4,BC=9. 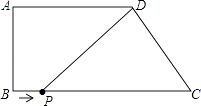
(1)求CD的长为 .
(2)点P从点B出发,以每秒1个单位的速度沿着边BC向点C运动,连接DP.设点P运动的时间为t秒,则当t为何值时,△PDC为等腰三角形?
【答案】
(1)5
(2)解:过点D作DE⊥BC,垂足为E,由题意得PC=9﹣t,PE=6﹣t.
当CD=CP时,5=9﹣t,解得t=4;
当CD=PD时,E为PC中点,
∴6﹣t=3,
∴t=3;
当PD=PC时,PD2=PC2,
∴(6﹣t)2+42=(9﹣t)2,
解得t= ![]() .
.
故t的值为t=3或4或 ![]() .
.
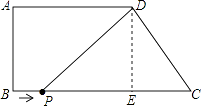
【解析】解:(1)过点D作DE⊥BC,垂足为E,∵AD∥BC,∠B=90°,
∴四边形ABED是矩形,
∴BE=AD=6,DE=AB=4,
∴CE=BC﹣BE=9﹣6=3,
在Rt△DCE中,CD= ![]() =
= ![]() =5.
=5.
所以答案是:5;
【考点精析】利用等腰三角形的判定和勾股定理的概念对题目进行判断即可得到答案,需要熟知如果一个三角形有两个角相等,那么这两个角所对的边也相等(简称:等角对等边).这个判定定理常用于证明同一个三角形中的边相等;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目