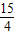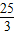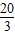题目内容
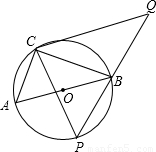
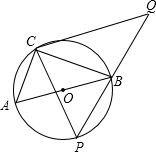 如图,在⊙O上有定点C和动点P,位于直径AB的异侧,过点C作CP的垂线,与PB的延长线交于点Q,已知:⊙O半径为
如图,在⊙O上有定点C和动点P,位于直径AB的异侧,过点C作CP的垂线,与PB的延长线交于点Q,已知:⊙O半径为 ,tan∠ABC=
,tan∠ABC= ,则CQ的最大值是
,则CQ的最大值是
- A.5
- B.

- C.

- D.

D
分析:根据圆周角定理的推论由AB为⊙O的直径得到∠ACB=90°,再根据正切的定义得到tan∠ABC= =
= ,然后根据圆周角定理得到∠A=∠P,则可证得△ACB∽△PCQ,利用相似比得CQ=
,然后根据圆周角定理得到∠A=∠P,则可证得△ACB∽△PCQ,利用相似比得CQ=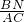 •PC=
•PC= PC,PC为直径时,PC最长,此时CQ最长,然后把PC=5代入计算即可.
PC,PC为直径时,PC最长,此时CQ最长,然后把PC=5代入计算即可.
解答:∵AB为⊙O的直径,
∴AB=5,∠ACB=90°,
∵tan∠ABC= ,
,
∴ =
= ,
,
∵CP⊥CQ,
∴∠PCQ=90°,
而∠A=∠P,
∴△ACB∽△PCQ,
∴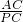 =
= ,
,
∴CQ= •PC=
•PC= PC,
PC,
当PC最大时,CQ最大,即PC为⊙O的直径时,CQ最大,此时CQ= ×5=
×5= .
.
故选D.
点评:本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.也考查了三角形相似的判定与性质.
分析:根据圆周角定理的推论由AB为⊙O的直径得到∠ACB=90°,再根据正切的定义得到tan∠ABC=
 =
= ,然后根据圆周角定理得到∠A=∠P,则可证得△ACB∽△PCQ,利用相似比得CQ=
,然后根据圆周角定理得到∠A=∠P,则可证得△ACB∽△PCQ,利用相似比得CQ=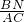 •PC=
•PC= PC,PC为直径时,PC最长,此时CQ最长,然后把PC=5代入计算即可.
PC,PC为直径时,PC最长,此时CQ最长,然后把PC=5代入计算即可.解答:∵AB为⊙O的直径,
∴AB=5,∠ACB=90°,
∵tan∠ABC=
 ,
,∴
 =
= ,
,∵CP⊥CQ,
∴∠PCQ=90°,
而∠A=∠P,
∴△ACB∽△PCQ,
∴
 =
= ,
,∴CQ=
 •PC=
•PC= PC,
PC,当PC最大时,CQ最大,即PC为⊙O的直径时,CQ最大,此时CQ=
 ×5=
×5= .
.故选D.
点评:本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.也考查了三角形相似的判定与性质.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目

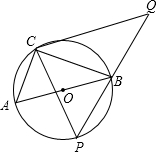 (2013•德阳)如图,在⊙O上有定点C和动点P,位于直径AB的异侧,过点C作CP的垂线,与PB的延长线交于点Q,已知:⊙O半径为
(2013•德阳)如图,在⊙O上有定点C和动点P,位于直径AB的异侧,过点C作CP的垂线,与PB的延长线交于点Q,已知:⊙O半径为
 ,tan∠ABC=
,tan∠ABC= ,则CQ的最大值是( )
,则CQ的最大值是( )