题目内容
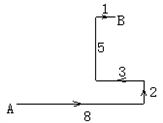
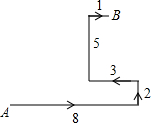如图所示，某人到一个荒岛上去探宝，在A处登陆后，往东走8km，又往北走2km，遇到障碍后又往西走3km，再折向北方走到5km处往东一拐，仅1km就找到了宝藏，问：登陆点（A处）到宝藏埋藏点（B处）的直线距离是多少？
分析：要求AB的长，需要构造到直角三角形中．连接AB，作BC垂直于过A的水平线于C．在直角三角形ABC中，得AC=8-3+1=6，BC=5+2=7．再运用勾股定理计算即可．
解答：解：过点B作BC⊥AC，垂足为C．
观察图形可知AC=AF-MF+MC=8-3+1=6，BC=2+5=7，
在Rt△ACB中，AB=
=
=
km．
答：登陆点到宝藏埋藏点的直线距离是
km．
观察图形可知AC=AF-MF+MC=8-3+1=6，BC=2+5=7，
在Rt△ACB中，AB=
| AC2+BC2 |
| 62+72 |
| 85 |
答：登陆点到宝藏埋藏点的直线距离是
| 85 |
点评：所求距离实际上就是AB的长．解此类题目的关键是构造直角三角形，利用勾股定理直接求解．
练习册系列答案
相关题目
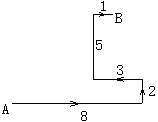
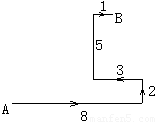
如图所示，某人到一个荒岛上去探宝，在A处登陆后，往东走8km，又往北走2km，遇到障碍后又往西走3km，再折向北方走到5km处往东一拐，仅1km就找到了宝藏，问：登陆点（A处）到宝藏埋藏点（B处）的直线距离是多少？