题目内容
【题目】在直角![]() 中,
中,![]() ,
,![]() ,AD,CE分别是
,AD,CE分别是![]() 和
和![]() 的平分线,AD,CE相交于点F.
的平分线,AD,CE相交于点F.
![]() 求
求![]() 的度数;
的度数;
![]() 判断FE与FD之间的数量关系,并证明你的结论.
判断FE与FD之间的数量关系,并证明你的结论.

【答案】(1)120°;(2)见解析.
【解析】
(1)由已知条件易得∠BAC=30°,结合AD,CE分别是∠BAC和∠ACB的角平分线可得∠FAC=15°,∠FCA=45°,由此结合三角形内角和定理可得∠AFC=120°,由此即可得到∠EFD=∠AFC=120°.
(2)如下图,在AC是截取AG=AE,连接FG,在由已知条件易证△AGF≌△AEF,由此可得∠AFG=∠AFE=∠FAC+∠ECA=60°,结合∠AFC=120°,可得∠CFG=60°,∠CFD=60°,这样结合∠GCF=∠DCF,CF=CF即可得到△GCF≌△DCF,由此可得FG=FD,结合FE=FG即可得到FE=FD.
(1)∵![]() 中,
中,![]() ,
,![]()
∴![]() ,
,
∵![]() 、CE分别是
、CE分别是![]() 、
、![]() 的平分线,
的平分线,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ;
;
![]() 与FD之间的数量关系为
与FD之间的数量关系为![]() ;
;
在AC上截取![]() ,连接FG,
,连接FG,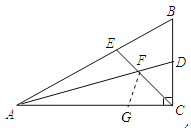
∵![]() 是
是![]() 的平分线,
的平分线,
∴![]()
在![]() 和
和![]() 中,∵
中,∵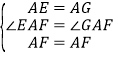 ,
,
∴![]() ≌
≌![]() ,
,
∴![]() ,∠AFG=∠AFE=∠FAC+∠ECA=60°,
,∠AFG=∠AFE=∠FAC+∠ECA=60°,
∴∠CFD=∠AFE=60°,
∴∠CFD=∠CFG,
∵在![]() 和
和![]() 中,
中,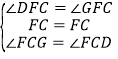 ,
,
∴![]() ≌
≌![]() ,
,
∴![]() ,
,
∴![]() .
.

 备战中考寒假系列答案
备战中考寒假系列答案【题目】列方程解应用题:五莲县新玛特购物中心第一次用5000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的![]() 倍多15件,甲、乙两种商品的进价和售价如下表(注:获利=售价﹣进价)
倍多15件,甲、乙两种商品的进价和售价如下表(注:获利=售价﹣进价)
甲 | 乙 | |
进价(元/件) | 20 | 30 |
售价(元/件) | 29 | 40 |
(1)新玛特购物中心将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(2)该购物中心第二次以第一次的进价又购进甲、乙两种商品,其中甲种商品的件数不变,乙种商品的件数是第一次的3倍;甲商品按原价销售,乙商品打折销售,第二次两种商品都销售完以后获得总利润比第一次获得的总利润多160元,求第二次乙种商品是按原价打几折销售?