Question

已知关于的一元二次方程有实数根，为正整数.
（1）求的值；
（2）当此方程有两个不为0的整数根时，将关于的二次函数的图象向下平移2个单位，求平移后的函数图象的解析式；
（3）在（2）的条件下，将平移后的二次函数图象位于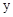轴左侧的部分沿轴翻折，图象的其余部分保持不变，得到一个新的图象G．当直线与图象G有3个公共点时，请你直接写出的取值范围.

Answer 1

(1) 1，2，3；（2）；（3）.

解析试题分析：(1)由求出正整数解即可.
（2）求出方程有两个不为0的整数根时的二次函数解析式，根据平移的性质得到平移后的函数图象的解析式.
（3）分直线与有一个交点且与有两个交点和直线与有两个交点且与有一个交点两种情况求解即可.
(1)∵ 方程有实数根，∴.
∴，解得.
∵为正整数，∴为1，2，3．
（2）当时，，方程的两个整数根为6，0；
当时，，方程无整数根；
当时，，方程的两个整数根为2，1
∴,原抛物线的解析式为： ．
∴平移后的图象的解析式为.
（3）翻折后得到一个新的图象G的解析式为，
联立得，即.
由得.
∴当或时，直线与有一个交点，当时，直线与有两个交点.
联立得，即.
由得.
∴当或时，直线与有一个交点，当时，直线与有两个交点.
∴要使直线与图象G有3个公共点即要直线与有一个交点且与有两个交点；或直线与有两个交点且与有一个交点.
∴的取值范围为.

考点：1．一元二次方程根的判别式；2.二次函数的平移；3.曲线上点的坐标与方程的关系；4.分类思想和数形结合思想的应用.