Question

在等腰直角△ABC中，AB=BC=5，P是△ABC内一点，且PA=，PC=5，则PB=________．

Answer 1

分析：先依据题意作一三角形，再结合图形进行分析，在等腰直角△ABC中，已知PA、PC，通过辅助线求出AD，DC及PD边的长，进而PB可求．
解答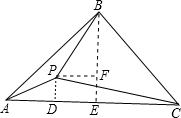：解：如图所示，过点B作BE⊥AC，过点P作PD，PF分别垂直AC，BE
在△APD中，PA²=PD²+AD²=5，
在△PCD中，PC²=PD²+CD²，且AD+CD=5，
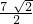解之得，AD=，CD=，PD=，
在Rt△ABC中，BE=AE=，
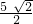所以在Rt△BPF中，PB²=PF²+BF²=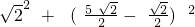=10，
所以PB=．
点评：熟练掌握勾股定理的运用．会画出简单的图形辅助解题．