题目内容
【题目】综合与实践:
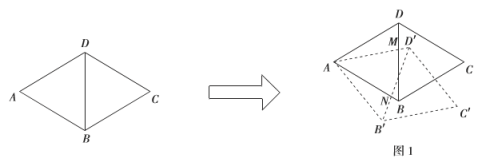
问题情境:在一次综合实践活动课上,同学们以菱形为对象,研究菱形旋转中的问题:已知,在菱形![]() 中,
中, ![]() 为对角线,
为对角线, ![]() ,
,![]() ,将菱形
,将菱形![]() 绕顶点
绕顶点![]() 顺时针旋转,旋转角为
顺时针旋转,旋转角为![]() (单位
(单位![]() ),旋转后的菱形为
),旋转后的菱形为![]() ,在旋转探究活动中提出下列问题,请你帮他们解决.
,在旋转探究活动中提出下列问题,请你帮他们解决.
观察证明:
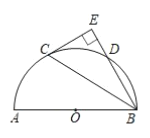
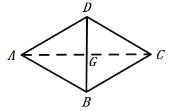
(1)如图1,若旋转角![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,请说明线段
,请说明线段![]() 与
与![]() 的数量关系;
的数量关系;
操作计算:
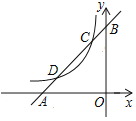
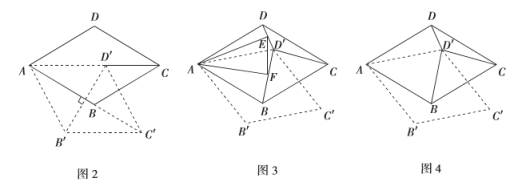
(2)如图2,连接![]() ,菱形
,菱形![]() 旋转的过程中,当
旋转的过程中,当![]() 与
与![]() 互相垂直时,
互相垂直时, ![]() 的长为 ;
的长为 ;
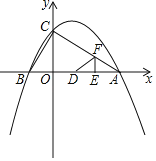
(3)如图3,若旋转角![]() ,分别连接
,分别连接![]() ,
,![]() ,过点
,过点![]() 分别作
分别作![]() ,
,![]() ,连接
,连接![]() ,菱形
,菱形![]() 旋转的过程中,发现在
旋转的过程中,发现在![]() 中存在长度不变的线段
中存在长度不变的线段![]() ,请求出
,请求出![]() 长度;
长度;
操作探究:
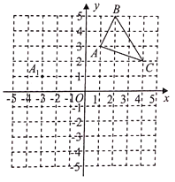
(4)如图4,在(3)的条件下,请判断以![]() ,
,![]() ,
,![]() 三条线段长度为边的三角形是什么特殊三角形,并说明理由.
三条线段长度为边的三角形是什么特殊三角形,并说明理由.
【答案】(1)![]() ,理由详见解析;(2)
,理由详见解析;(2)![]() ;(3)2;(4)以
;(3)2;(4)以![]() ,
,![]() ,
,![]() 三条线段为边的三角形是直角三角形,理由详见解析.
三条线段为边的三角形是直角三角形,理由详见解析.
【解析】
(1)根据菱形的性质以及旋转的性质,证得![]() ,根(
,根(![]() 证得
证得![]() ≌
≌![]() ,可以得到结论;
,可以得到结论;
(2)根据菱形的性质以及条件![]() 与
与![]() 互相垂直,证明
互相垂直,证明![]() 、
、![]() 在同一直线上,利用锐角三角函数求得对角线的长,继而求得结论;
在同一直线上,利用锐角三角函数求得对角线的长,继而求得结论;
(3)利用等腰三角形三线合一的性质,![]() 是
是![]() 的中位线,从而证明
的中位线,从而证明![]() ;
;
(4) 以![]() 为边向外作等边三角形,利用等边三角形的性质以及
为边向外作等边三角形,利用等边三角形的性质以及![]() 证得
证得![]() ≌
≌![]() ,得到
,得到![]() ,把
,把![]() ,
,![]() ,
,![]() 三条线段归结到一个三角形中,易证得
三条线段归结到一个三角形中,易证得![]() 是直角三角形,从而得到结论.
是直角三角形,从而得到结论.
(1) ![]() ,理由如下:
,理由如下:
∵四边形![]() 是菱形
是菱形
∴![]()
∴![]()
由旋转的性质可得: ![]() ,
,![]() ,
,![]() ,
,![]()
∴![]()
∴![]()
即![]()
在![]() 和
和![]() 中
中
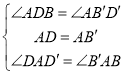
∴![]() ≌
≌![]() (
(![]() )
)
∴![]()
(2) 菱形![]() 中,
中, ![]() ,
, ![]() ,
,
∴![]() 平分
平分![]() (等腰三角形三线合一),
(等腰三角形三线合一),
∴![]() ,
,
∵![]() ,
,
∴![]()
∴![]() 、
、![]() 在同一直线上,
在同一直线上,
如图,菱形![]() 中,
中, ![]() 为对角线,
为对角线, ![]() ,
,![]() ,
,
∴![]() ,
,![]()
∴![]()
∴![]()
∴![]()
故答案是:![]()
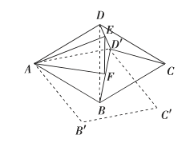
(3)如图,连接![]() ,由题可得:
,由题可得: ![]()
∵![]()
∴![]() (等腰三角形三线合一),同理
(等腰三角形三线合一),同理![]()
∴![]() 是
是![]() 的中位线
的中位线
∴![]()
∵四边形![]() 是菱形
是菱形
∴![]()
又∵![]() ,
,![]() 是等边三角形
是等边三角形
∴![]()
∴![]()
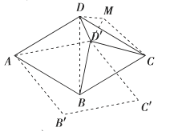
(4)以![]() ,
,![]() ,
,![]() 三条线段为边的三角形是直角三角形,理由如下:
三条线段为边的三角形是直角三角形,理由如下:
如图,以![]() 为边向外作等边三角形
为边向外作等边三角形![]() ,连接
,连接![]() ,
,![]()
∵四边形![]() 是菱形,
是菱形, ![]()
∴![]() 与
与![]() 是等边三角形,
是等边三角形, ![]()
由(3)可知: ![]() 与
与![]() 都是等腰三角形
都是等腰三角形
∴![]()
![]()
∵![]() 与
与![]() 是等边三角形
是等边三角形
∴![]() ,
,![]() ,
,![]()
∴![]()
∴![]()
在![]() 和
和![]() 中
中

∴![]() ≌
≌![]() (
(![]() )
)
∴![]() ,
,![]()
∴![]()
∴![]() 是直角三角形
是直角三角形
即以![]() ,
,![]() ,
,![]() 三条线段长度为边的三角形是直角三角形.
三条线段长度为边的三角形是直角三角形.

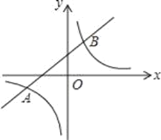
【题目】小明利用函数与不等式的关系,对形如![]() (
(![]() 为正整数)的不等式的解法进行了探究.
为正整数)的不等式的解法进行了探究.
(1)下面是小明的探究过程,请补充完整:
①对于不等式![]() ,观察函数
,观察函数![]() 的图象可以得到如下表格:
的图象可以得到如下表格:
|
|
|
|
|
|
由表格可知不等式![]() 的解集为
的解集为![]() .
.
②对于不等式![]() ,观察函数
,观察函数![]() 的图象可得到如下表格:
的图象可得到如下表格:
|
|
|
|
|
|
|
|
由表格可知不等式![]() 的解集为 .
的解集为 .
③对于不等式![]() ,请根据已描出的点画出函数
,请根据已描出的点画出函数![]() 的图象;
的图象;
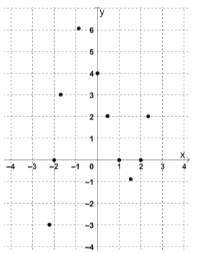
观察函数![]() 的图象,
的图象,
补全下面的表格:
|
|
|
|
|
|
|
|
由表格可知不等式![]() 的解集为 .
的解集为 .
小明将上述探究过程总结如下:对于解形如![]() (
(![]() 为正整数)的不等式,先将
为正整数)的不等式,先将![]() 按从大到小的顺序排列,再划分
按从大到小的顺序排列,再划分![]() 的范围,然后通过列表格的办法,可以发现表格中
的范围,然后通过列表格的办法,可以发现表格中![]() 的符号呈现一定的规律,利用这个规律可以求这样的不等式的解集.
的符号呈现一定的规律,利用这个规律可以求这样的不等式的解集.
(2)请你参考小明的方法,解决下列问题:
①不等式![]() 的解集为 .
的解集为 .
②不等式![]() 的解集为 .
的解集为 .