题目内容
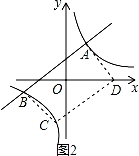
如图,双曲线y=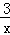 与直线y=
与直线y= x+1交于A、B两点,A点在B点的右侧.
x+1交于A、B两点,A点在B点的右侧.
(1)求A、B点的坐标;
(2)点C是双曲线上一点,点D是x轴上一点,是否存在点D,使以A、B、C、D为顶点的四边形是平行四边形?如果存在,写出求解过程和点D的坐标;若不存在,请说明理由.
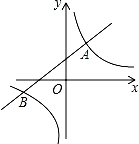
【考点】反比例函数综合题.
【分析】(1)联立一次函数与反比例函数的解析式即可得出A、B两点的坐标;
(2)根据AB两点的坐标可求出线段AB的水平距离与竖直距离,再根据AB为平行四边形的边与对角线两种情况进行讨论即可.
【解答】解:(1)由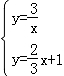 消去y得,2x2+3x﹣9=0,
消去y得,2x2+3x﹣9=0,
解得x1=﹣3,x2=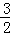 ,
,
点A的坐标为(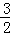 ,2),点B的坐标为(﹣3,﹣1).
,2),点B的坐标为(﹣3,﹣1).
(2)∵A(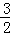 ,2),B(﹣3,﹣1),
,2),B(﹣3,﹣1),
∴线段AB的垂直距离为2﹣(﹣1)=3,水平距离为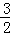 ﹣(﹣3)=
﹣(﹣3)=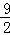 .
.
①令y=3,由y=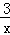 得x=1,则1﹣
得x=1,则1﹣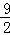 =﹣
=﹣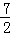 ,
,
∴点D的坐标(﹣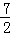 ,0);
,0);
②令y=﹣3,由y=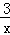 得x=﹣1,则﹣1+
得x=﹣1,则﹣1+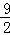 =
=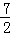 ,
,
∴点D的坐标(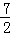 ,0);
,0);
③如图,线段AB的中点E的坐标为(﹣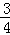 ,
,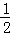 ),过点C作CF⊥x轴于点G,点E作EG⊥OF于x轴点G,
),过点C作CF⊥x轴于点G,点E作EG⊥OF于x轴点G,
则EG=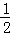 ,
,
∵EG是△CDF的中位线
∴CF=2EG=1,即F点的纵坐标为1,
∴C(3,1),
∴F(3,0).
∴DG=GF,即3+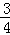 =﹣
=﹣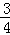 ﹣x,解得x=﹣
﹣x,解得x=﹣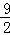 .
.
点D的坐标(﹣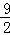 ,0).
,0).
综上所述,D点坐标为(﹣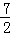 ,0),(
,0),(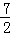 ,0)或(﹣
,0)或(﹣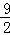 ,0
,0 ).
).


【点评】本题考查的是反比例函数综合题,涉及到反比例函数图象上点的坐标特点、平行四边形的判定与性质等知识,在解答(2)时要注意进行分类讨论.

练习册系列答案
相关题目

 B.
B.



 B.
B. C.
C. D.
D.

 B.
B. C.
C. D.
D.