题目内容
 (2013•海陵区模拟)已知点A是双曲线y=
(2013•海陵区模拟)已知点A是双曲线y=| 3 |
| x |
y=-
(x≠0)
| 9 |
| x |
y=-
(x≠0)
.| 9 |
| x |
分析:设点A的坐标为(a,
),连接OC,则OC⊥AB,表示出OC,过点C作CD⊥x轴于点D,设出点C坐标,在Rt△OCD中,利用勾股定理可得出x2的值,继而得出y与x的函数关系式.
| 3 |
| a |
解答:解:设A(a,
),
∵点A与点B关于原点对称,
∴OA=OB,
∵△ABC为等边三角形,
∴AB⊥OC,OC=
AO,
∵AO=
,
∴CO=
,

过点C作CD⊥x轴于点D,
则可得∠AOD=∠OCD(都是∠COD的余角),
设点C的坐标为(x,y),则tan∠AOD=tan∠OCD,即
=
,
解得:y=-
x,
在Rt△COD中,CD2+OD2=OC2,即y2+x2=3a2+
,
将y=-
x代入,可得:x2=
,
故x=
,y=-
x=-
a,
则xy=-9,
故可得:y=-
(x≠0).
故答案为:y=-
(x≠0).
| 3 |
| a |
∵点A与点B关于原点对称,
∴OA=OB,
∵△ABC为等边三角形,
∴AB⊥OC,OC=
| 3 |
∵AO=
a2+(
|
∴CO=
3a2+
|

过点C作CD⊥x轴于点D,
则可得∠AOD=∠OCD(都是∠COD的余角),
设点C的坐标为(x,y),则tan∠AOD=tan∠OCD,即
| ||
| a |
| x |
| -y |
解得:y=-
| a2 |
| 3 |
在Rt△COD中,CD2+OD2=OC2,即y2+x2=3a2+
| 27 |
| a2 |
将y=-
| a2 |
| 3 |
| 27 |
| a2 |
故x=
3
| ||
| a |
| a2 |
| 3 |
| 3 |
则xy=-9,
故可得:y=-
| 9 |
| x |
故答案为:y=-
| 9 |
| x |
点评:本题考查了反比例函数的综合题,涉及了解直角三角形、等边三角形的性质及勾股定理的知识,综合考察的知识点较多,解答本题的关键是将所学知识融会贯通,注意培养自己解答综合题的能力.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
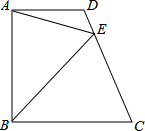 (2013•海陵区模拟)已知直角梯形ABCD中,AD∥BC,∠ABC=90°,AD=8,AB=12,BC=13,E为CD上一点,BE=13,则S△ADE:S△BEC是( )
(2013•海陵区模拟)已知直角梯形ABCD中,AD∥BC,∠ABC=90°,AD=8,AB=12,BC=13,E为CD上一点,BE=13,则S△ADE:S△BEC是( )