题目内容
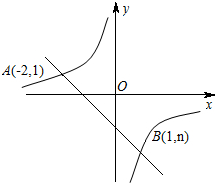
已知如图,一次函数y=kx+b的图象与反比例函数![]() 的图象相交于A、B两点.
的图象相交于A、B两点.
(1)利用图中条件,求反比例函数和一次函数的解析式;
(2)根据图象写出使一次函数的值大于反比例函数的值的x的取值范围.

考点:
反比例函数与一次函数的交点问题..
专题:
代数综合题;数形结合.
分析:
(1)利用已知求出反比例函数的解析式,再利用两函数交点求出一次函数解析式;
(2)利用函数图象求出分别得出使一次函数的值大于反比例函数的值的x的取值范围.
解答:
解:(1)据题意,反比例函数![]() 的图象经过点A(﹣2,1)
的图象经过点A(﹣2,1)
∴有m=xy=﹣2
∴反比例函数解析式为y=﹣,
又反比例函数的图象经过点B(1,n)
∴n=﹣2,
∴B(1,﹣2)
将A、B两点代入y=kx+b有![]() ,
,
解得![]() ,
,
∴一次函数的解析式为y=﹣x﹣1,
(2)根据图象写出使一次函数的值大于反比例函数的值的x的取值范围为:
x取相同值,一次函数图象在反比例函数上方即一次函数大于反比例函数,
∴x<﹣2或0<x<1,
点评:
此题主要考查了待定系数法求反比例函数解析式以及待定系数法求一次函数解析式,利用图象判定函数的大小关系是中学的难点同学们应重点掌握.

练习册系列答案
相关题目
 已知如图,一次函数y=kx+b的图象与反比例函数
已知如图,一次函数y=kx+b的图象与反比例函数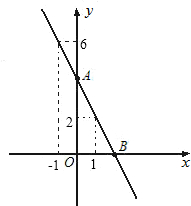 已知如图,一次函数y=ax+b图象经过点(1,2)、点(-1,6).求:
已知如图,一次函数y=ax+b图象经过点(1,2)、点(-1,6).求: 于3?如果能,求此时抛物线的解析式;如果不能,请说明理由.
于3?如果能,求此时抛物线的解析式;如果不能,请说明理由.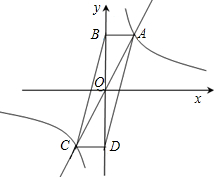 已知如图:一次函数y=2x与反比例函数
已知如图:一次函数y=2x与反比例函数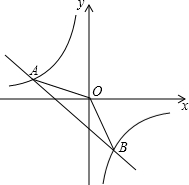 B(1,n)两点.
B(1,n)两点.