Question

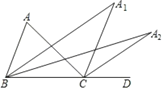
【题目】如图，∠ACD是△ABC的外角，∠ABC的平分线与∠ACD的平分线交于点A1,∠A1BC的平分线与∠A1CD的平分线交于点A2，∠A2BC的平分线与∠A2CD的平分线交于点A3.设∠A=64°.则（1）∠A1=________；（2）∠A3=_______。

Answer 1

【答案】32° 8°

【解析】

根据角平分线的定义可得∠A1BC＝∠ABC，∠A1CD＝∠ACD，再根据三角形的一个外角等于与它不相邻的两个内角的和可得∠ACD＝∠A＋∠ABC，∠A1CD＝∠A1BC＋∠A1，整理即可求出∠A1＝∠A＝32°，同理可求出∠A2和∠A3.

解：∵BA1是∠ABC的平分线，CA1是∠ACD的平分线，

∴∠A1BC＝∠ABC，∠A1CD＝∠ACD，

又∵∠ACD＝∠A＋∠ABC，∠A1CD＝∠A1BC＋∠A1，

∴（∠A＋∠ABC）＝∠ABC＋∠A1，

∴∠A1＝∠A＝32°，

同理可得：∠A2＝∠A1＝16°，∠A3＝∠A2＝8°，

故答案为：32°，8°.