题目内容
已知四边形OABC是边长为4的正方形,分别以OA、OC所在的直线为x轴、y轴,建立如图1所示的平面直角坐标系,直线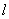 经过A、C两点.
经过A、C两点.
(1)写出点A、点C坐标并求直线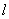 的函数表达式;
的函数表达式;
(2)若P是直线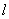 上的一点,当△OPA的面积是5时,请求出点P的坐标;
上的一点,当△OPA的面积是5时,请求出点P的坐标;
(3)如图2,点D(3,-1),E是直线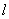 上的一个动点,求出使|BE-DE|取得最大值时点E的坐标和最大值(不需要证明).
上的一个动点,求出使|BE-DE|取得最大值时点E的坐标和最大值(不需要证明).
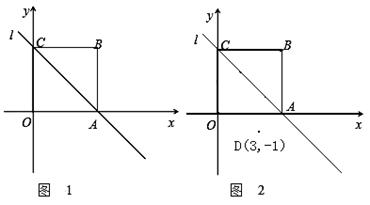
解:(1)A(4,0)和C(0,4)…………………………2分
设直线l的函数表达式y=kx+b(k≠0),经过A(4,0)和C(0,4)
得 ,
,
解之得 ,
,
∴直线l的函数表达式y=﹣x+4; ………………………………………4分
(2)设△OPA底边OA上的高为h,由题意等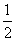 ×4×h=5,∴h=
×4×h=5,∴h=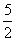
∴|-x+4|=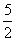 ,解得x=
,解得x= 或
或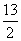
∴P1( ,
,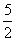 )、P2(
)、P2(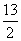 ,
,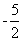 )……………………………………………….…6分
)……………………………………………….…6分
(3)∵O与B关于直线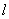 对称,
对称,
∴连接OD并延长交直线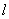 于点E,则点E为所求,此时|BE-DE|=|OE-DE|=OD,OD即为最大值。
于点E,则点E为所求,此时|BE-DE|=|OE-DE|=OD,OD即为最大值。
设OD所在直线为y=k1x (k1≠0),经过点D(3,-1),∴-1=3k1 , ∴k1=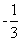
∴直线OD为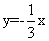 , ……………………………………….……8分
, ……………………………………….……8分
解方程组: 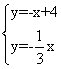 ,得
,得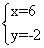 ,
,
∴点E的坐标为(6,-2). ……………………9分
又D点的坐标为(3,-1)
由勾股地理可得OD=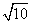 …………………10分
…………………10分


某校开展“人人会乐器”的活动,根据实际开设了四种乐器的相关课程.学校为了了解学生最喜欢哪一种乐器(每位学生只能选一类),随机抽取了部分学生进行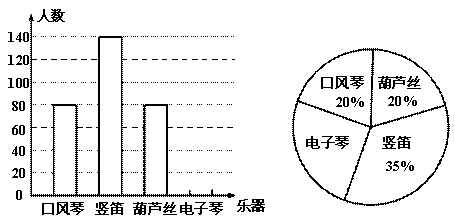 调查,并将调查结果绘制成如下统计图.
调查,并将调查结果绘制成如下统计图.
|
请你根据图中提供的信息,回答下列问题:
(1)总共随机抽查了多少位学生?请你把条形统计图补全.
(2)样本中喜欢电子琴的人数比喜欢葫芦丝的多______人。
(3)该校一共有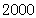 名学生,你认为全校喜欢哪种乐器的学生人最多?估计有多少人?
名学生,你认为全校喜欢哪种乐器的学生人最多?估计有多少人?
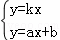 的解是 .
的解是 .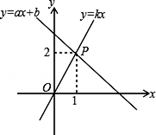

 A.
A.  B.
B.  C.
C.  D.
D.