题目内容
已知:如图, 是
是 的直径,
的直径, ,
,  切
切 于点
于点 垂足为
垂足为
 交
交 于点
于点 .
.

1.求证: ;
;
2.若 , 求
, 求 的长
的长
【答案】
1.证明:连结
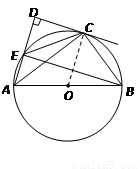
由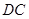 是切线得
是切线得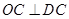 -------------------------------1分
-------------------------------1分
又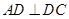
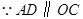
∴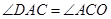
又由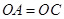 得
得
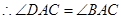
∴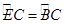
∴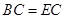 --------------------------------------------4分
--------------------------------------------4分
2.解: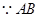 为直径
为直径
∴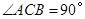 --------------------------------------------5分
--------------------------------------------5分
又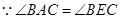
∴ 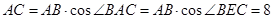
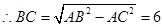 --------------------------7分
--------------------------7分
∴ 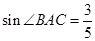 ----------------------------------8分
----------------------------------8分
又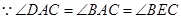 且
且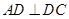
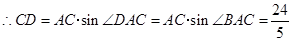 --------10分
--------10分
【解析】(1)连接OC.根据切线的性质,得OC⊥DC,结合已知条件,得AD∥OC,根据两条直线平行,内错角相等,得∠DAC=∠ACO,再根据同圆的半径相等,得∠BAC=∠ACO,从而得到∠DAC=∠BAC,再根据圆周角定理得到它们所对的弧相等,进一步得到弧所对的弦相等;
(2)根据直径所对的圆周角是直角,得到直角三角形ABC.根据圆周角定理,得∠BAC=∠BEC,从而利用解直角三角形的知识求得BC的长,再利用CD=AC•sin∠DAC求解.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
 是
是 的直径,
的直径, 切
切 ,
, 交
交 ,
, 为
为 .
. ,
,
 是
是 的直径,弦
的直径,弦 ,垂足为
,垂足为 ,
,
 .
.
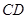 的长;
的长;