题目内容
(1)计算: ;
;
(2)先化简,代数式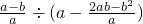 ,然后选择合适的a、b值代入求值.
,然后选择合适的a、b值代入求值.
解:(1)原式= +
+ ×1-
×1- ×
× ,
,
= ,
,
= ;
;
(2)原式= ÷(
÷( ),
),
= ×
× ,
,
= .
.
∵a≠0,a-b≠0
∴当a=2,b=3时,分式有意义.
∴当a=2,b=3时,原式= =-1.
=-1.
分析:(1)因为 -1的有理化因式是
-1的有理化因式是 +1,所以对
+1,所以对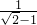 分子分母同乘以
分子分母同乘以 +1,即可化简;再利用a0=1(a≠0),对后面(2008-
+1,即可化简;再利用a0=1(a≠0),对后面(2008- )的0次幂进行化简即可;
)的0次幂进行化简即可;
(2)利用分式的混合运算法则,先把原分式化简,再取使分式有意义的a、b值代入求值即可.
点评:(1)本题考查了二次根式的混合运算,在运算时注意公式a0=1(a≠0)的运用.
(2)本题考查了分式的化简求值,在化简时注意因式分解的运用,给未知数取值时要保证分母不为0.
 +
+ ×1-
×1- ×
× ,
,=
 ,
,=
 ;
;(2)原式=
 ÷(
÷( ),
),=
 ×
× ,
,=
 .
.∵a≠0,a-b≠0
∴当a=2,b=3时,分式有意义.
∴当a=2,b=3时,原式=
 =-1.
=-1.分析:(1)因为
 -1的有理化因式是
-1的有理化因式是 +1,所以对
+1,所以对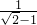 分子分母同乘以
分子分母同乘以 +1,即可化简;再利用a0=1(a≠0),对后面(2008-
+1,即可化简;再利用a0=1(a≠0),对后面(2008- )的0次幂进行化简即可;
)的0次幂进行化简即可;(2)利用分式的混合运算法则,先把原分式化简,再取使分式有意义的a、b值代入求值即可.
点评:(1)本题考查了二次根式的混合运算,在运算时注意公式a0=1(a≠0)的运用.
(2)本题考查了分式的化简求值,在化简时注意因式分解的运用,给未知数取值时要保证分母不为0.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
