题目内容
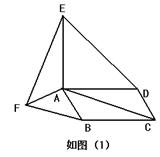
探究:如图(1),在?ABCD的形外分别作等腰直角△ABF和等腰直角△ADE,∠FAB=∠EAD=90°,连接AC,EF.在图中找一个与△FAE全等的三角形,并加以证明.应用:以?ABCD的四条边为边,在其形外分别作正方形,如图(2),连接EF,GH,IJ,KL.若?ABCD的面积为6,则图中阴影部分四个三角形的面积和为______.
推广:以?ABCD的四条边为矩形长边,在其形外分别作长与宽之比为
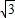 矩形,如图(3),连接EF,GH,IJ,KL.若图中阴影部分四个三角形的面积和为12
矩形,如图(3),连接EF,GH,IJ,KL.若图中阴影部分四个三角形的面积和为12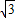 ,求?ABCD的面积?
,求?ABCD的面积?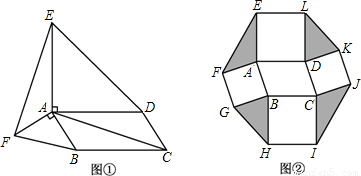
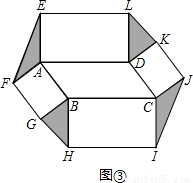
【答案】分析:探究:求出AF=AB,AE=AD=BC,∠FAE=∠ABC,根据SAS推出两三角形全等即可;
应用:过B作BO⊥AD于O,BS⊥CD于S,过E作EQ⊥FA,交FA延长线于Q,过K作KW⊥LD于W,过I作IZ⊥JC交JC的延长线于Z,过G作GR⊥BH于R,根据平行四边形的面积得出S平行四边形ABCD=AD×BO=CD×BS=6,根据平行四边形的性质得出AD=BC,AB=CD,∠BAD=∠BCD,求出∠EAQ=∠BAD=∠BCS,证△EQA≌△BSC,求出EQ=BS,求出AF×EQ=CD×BS=6,推出S△EAF= AF×EQ=3,同理S△CIJ=3,SLDK=
AF×EQ=3,同理S△CIJ=3,SLDK= LD×KW=
LD×KW= AD×BO=
AD×BO= ×6=3,即可得出答案;
×6=3,即可得出答案;
推广:过B作BO⊥AD于O,BS⊥CD于S,过E作EQ⊥FA,交FA延长线于Q,过K作KW⊥LD于W,求出S平行四边形ABCD=AD×BO=CD×BS,设AD=BC=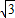 a,AB=CD=
a,AB=CD=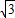 b,∠BAD=∠BCD,求出∠EAQ=∠BAD=∠BCS,∠Q=∠BSC=90°,证△EQA∽△BSC,求出BS=
b,∠BAD=∠BCD,求出∠EAQ=∠BAD=∠BCS,∠Q=∠BSC=90°,证△EQA∽△BSC,求出BS=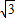 EQ,求出S平行四边形ABCD=6S△EAF,同理S平行四边形ABCD=6S△LDK=6S△GBH=6S△ICJ,求出S△EAF=S△LDK=S△GBH=S△ICJ=3
EQ,求出S平行四边形ABCD=6S△EAF,同理S平行四边形ABCD=6S△LDK=6S△GBH=6S△ICJ,求出S△EAF=S△LDK=S△GBH=S△ICJ=3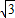 ,即可得出答案.
,即可得出答案.
解答:探究:△ABC或△ADC,
证明:∵△AFB和△ADE是等腰直角三角形,
∴AF=AB,AE=AD,∠FAB=∠EAD=90°,
∴∠FAE+∠DAB=360°-90°-90°=180°,
∵四边形ABCD是平行四边形,
∴AD=BC=AE,AB=CD=AF,AD∥BC,
∴∠DAB+∠ABC=180°,
∴∠FAE=∠ABC,
 在△FAE和△ABC中
在△FAE和△ABC中
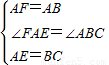 ,
,
∴△FAE≌△ABC,
同法可求△FAE≌△CDA;
应用:
解:过B作BO⊥AD于O,BS⊥CD于S,过E作EQ⊥FA,交FA延长线于Q,过K作KW⊥LD于W,过I作IZ⊥JC交JC的延长线于Z,过G作GR⊥BH于R,
则∠Q=∠BSC=90°,S平行四边形ABCD=AD×BO=CD×BS=6,
∵四边形ABCD是平行四边形,
∴设AD=BC=a,AB=CD=b,∠BAD=∠BCD,
∵四边形ABGF、四边形BCIH、四边形CDKJ、四边形ADKL是正方形,
∴AE=AD=BC,DK=CD=AB,∠EAD=∠FAB=90°,
∴∠EAF+∠BAD=360°-90°-90°=180°,
∵∠EAQ+∠EAF=180°,
∴∠EAQ=∠BAD=∠BCS,
在△EQA和△BSC中
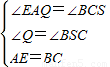 ,
,
∴△EQA≌△BSC,
∴EQ=BS,
∵AF=AB=CD,
∴AF×EQ=CD×BS=6,
∴S△EAF= AF×EQ=
AF×EQ= ×6=3,
×6=3,
同理S△CIJ=3,SLDK= LD×KW=
LD×KW= AD×BO=
AD×BO= ×6=3,
×6=3,
S△GBH=3,
∴图中阴影部分四个三角形的面积和为3+3+3+3=12,
故答案为:12;
推广:
解:B作BO⊥AD于O,BS⊥CD于S,过E作EQ⊥FA,交FA延长线于Q,过K作KW⊥LD于W,
则∠Q=∠BSC=90°,S平行四边形ABCD=AD×BO=CD×BS,
∵四边形ABCD是平行四边形,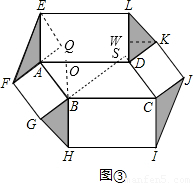
∴设AD=BC=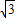 a,AB=CD=
a,AB=CD=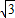 b,∠BAD=∠BCD,
b,∠BAD=∠BCD,
∵四边形ABGF、四边形BCIH、四边形CDKJ、四边形ADKL是矩形,
∴AE=DL=a,AF=BG=b,∠EAD=∠FAB=90°,
∴∠EAF+∠BAD=360°-90°-90°=180°,
∵∠EAQ+∠EAF=180°,
∴∠EAQ=∠BAD=∠BCS,
∠Q=∠BSC=90°,
∴△EQA∽△BSC,
∴ =
=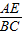 =
=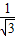 ,
,
∴BS=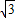 EQ,
EQ,
∵AF=b,AD= a,AF=b,
a,AF=b,
∴S△EAF= AF×EQ=
AF×EQ= b•EQ,
b•EQ,
∵S平行四边形ABCD=AB×BS=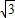 b•
b• EQ=3×2×
EQ=3×2× b•EQ=6S△EAF,
b•EQ=6S△EAF,
同理S平行四边形ABCD=6S△LDK=6S△GBH=6S△ICJ,
∴S△EAF=S△LDK=S△GBH=S△ICJ,
∵图中阴影部分四个三角形的面积和为12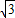 ,
,
∴S△EAF=S△LDK=S△GBH=S△ICJ=3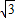 ,
,
∴平行四边形ABCD的面积是6×3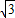 =18
=18 .
.
点评:本题考查了平行四边形性质,等腰直角三角形的性质,全等三角形的性质和判定的应用,主要考查学生的推理能力和计算能力,题目比较好,求解过程类似.
应用:过B作BO⊥AD于O,BS⊥CD于S,过E作EQ⊥FA,交FA延长线于Q,过K作KW⊥LD于W,过I作IZ⊥JC交JC的延长线于Z,过G作GR⊥BH于R,根据平行四边形的面积得出S平行四边形ABCD=AD×BO=CD×BS=6,根据平行四边形的性质得出AD=BC,AB=CD,∠BAD=∠BCD,求出∠EAQ=∠BAD=∠BCS,证△EQA≌△BSC,求出EQ=BS,求出AF×EQ=CD×BS=6,推出S△EAF=
 AF×EQ=3,同理S△CIJ=3,SLDK=
AF×EQ=3,同理S△CIJ=3,SLDK= LD×KW=
LD×KW= AD×BO=
AD×BO= ×6=3,即可得出答案;
×6=3,即可得出答案;推广:过B作BO⊥AD于O,BS⊥CD于S,过E作EQ⊥FA,交FA延长线于Q,过K作KW⊥LD于W,求出S平行四边形ABCD=AD×BO=CD×BS,设AD=BC=
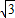 a,AB=CD=
a,AB=CD=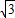 b,∠BAD=∠BCD,求出∠EAQ=∠BAD=∠BCS,∠Q=∠BSC=90°,证△EQA∽△BSC,求出BS=
b,∠BAD=∠BCD,求出∠EAQ=∠BAD=∠BCS,∠Q=∠BSC=90°,证△EQA∽△BSC,求出BS=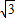 EQ,求出S平行四边形ABCD=6S△EAF,同理S平行四边形ABCD=6S△LDK=6S△GBH=6S△ICJ,求出S△EAF=S△LDK=S△GBH=S△ICJ=3
EQ,求出S平行四边形ABCD=6S△EAF,同理S平行四边形ABCD=6S△LDK=6S△GBH=6S△ICJ,求出S△EAF=S△LDK=S△GBH=S△ICJ=3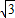 ,即可得出答案.
,即可得出答案.解答:探究:△ABC或△ADC,
证明:∵△AFB和△ADE是等腰直角三角形,
∴AF=AB,AE=AD,∠FAB=∠EAD=90°,
∴∠FAE+∠DAB=360°-90°-90°=180°,
∵四边形ABCD是平行四边形,
∴AD=BC=AE,AB=CD=AF,AD∥BC,
∴∠DAB+∠ABC=180°,
∴∠FAE=∠ABC,
 在△FAE和△ABC中
在△FAE和△ABC中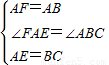 ,
,∴△FAE≌△ABC,
同法可求△FAE≌△CDA;
应用:
解:过B作BO⊥AD于O,BS⊥CD于S,过E作EQ⊥FA,交FA延长线于Q,过K作KW⊥LD于W,过I作IZ⊥JC交JC的延长线于Z,过G作GR⊥BH于R,
则∠Q=∠BSC=90°,S平行四边形ABCD=AD×BO=CD×BS=6,
∵四边形ABCD是平行四边形,
∴设AD=BC=a,AB=CD=b,∠BAD=∠BCD,
∵四边形ABGF、四边形BCIH、四边形CDKJ、四边形ADKL是正方形,
∴AE=AD=BC,DK=CD=AB,∠EAD=∠FAB=90°,
∴∠EAF+∠BAD=360°-90°-90°=180°,
∵∠EAQ+∠EAF=180°,
∴∠EAQ=∠BAD=∠BCS,
在△EQA和△BSC中
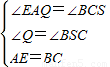 ,
,∴△EQA≌△BSC,
∴EQ=BS,
∵AF=AB=CD,
∴AF×EQ=CD×BS=6,
∴S△EAF=
 AF×EQ=
AF×EQ= ×6=3,
×6=3,同理S△CIJ=3,SLDK=
 LD×KW=
LD×KW= AD×BO=
AD×BO= ×6=3,
×6=3,S△GBH=3,
∴图中阴影部分四个三角形的面积和为3+3+3+3=12,
故答案为:12;
推广:
解:B作BO⊥AD于O,BS⊥CD于S,过E作EQ⊥FA,交FA延长线于Q,过K作KW⊥LD于W,
则∠Q=∠BSC=90°,S平行四边形ABCD=AD×BO=CD×BS,
∵四边形ABCD是平行四边形,

∴设AD=BC=
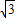 a,AB=CD=
a,AB=CD=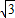 b,∠BAD=∠BCD,
b,∠BAD=∠BCD,∵四边形ABGF、四边形BCIH、四边形CDKJ、四边形ADKL是矩形,
∴AE=DL=a,AF=BG=b,∠EAD=∠FAB=90°,
∴∠EAF+∠BAD=360°-90°-90°=180°,
∵∠EAQ+∠EAF=180°,
∴∠EAQ=∠BAD=∠BCS,
∠Q=∠BSC=90°,
∴△EQA∽△BSC,
∴
 =
=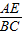 =
=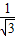 ,
,∴BS=
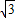 EQ,
EQ,∵AF=b,AD=
 a,AF=b,
a,AF=b,∴S△EAF=
 AF×EQ=
AF×EQ= b•EQ,
b•EQ,∵S平行四边形ABCD=AB×BS=
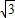 b•
b• EQ=3×2×
EQ=3×2× b•EQ=6S△EAF,
b•EQ=6S△EAF,同理S平行四边形ABCD=6S△LDK=6S△GBH=6S△ICJ,
∴S△EAF=S△LDK=S△GBH=S△ICJ,
∵图中阴影部分四个三角形的面积和为12
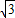 ,
,∴S△EAF=S△LDK=S△GBH=S△ICJ=3
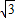 ,
,∴平行四边形ABCD的面积是6×3
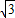 =18
=18 .
.点评:本题考查了平行四边形性质,等腰直角三角形的性质,全等三角形的性质和判定的应用,主要考查学生的推理能力和计算能力,题目比较好,求解过程类似.

练习册系列答案
相关题目



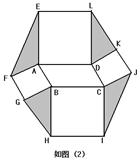
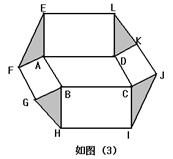
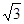 矩形,如图(3),连接EF,GH,IJ,KL。若图中阴影部分四个三角形的面积和为12
矩形,如图(3),连接EF,GH,IJ,KL。若图中阴影部分四个三角形的面积和为12 ,求
,求 的值.
的值. 
 ,那么
,那么
 ,那么
,那么 的值为 (用含m,n的代数式表示).
的值为 (用含m,n的代数式表示).

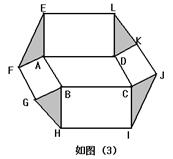
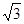 矩形,如图(3),连接EF,GH,IJ,KL。若图中阴影部分四个三角形的面积和为12
矩形,如图(3),连接EF,GH,IJ,KL。若图中阴影部分四个三角形的面积和为12