题目内容
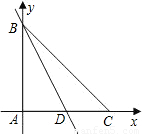
(2006•漳州)已知△ABC,∠BAC=90°,AB=AC=4,BD是AC边上的中线,分别以AC,AB所在直线为x轴,y轴建立直角坐标系(如图).(1)在BD所在直线上找出一点P,使四边形ABCP为平行四边形,画出这个平行四边形,并简要叙述其过程;
(2)求直线BD的函数关系式;
(3)直线BD上是否存在点M,使△AMC为等腰三角形?若存在,求点M的坐标;若不存在,说明理由.
【答案】分析:(1)因为BD是AC边上的中线,所以过A画AP∥BC,交直线BD于P,连接PC,可得到△ADP≌△CDB.
即可得到BD=CD.利用对角线互相平分的四边形是平行四边形可知四边形ABCP是所画的平行四边形;
(2)因为AB=AC=4,BD是AC边上的中线,所以可得到AD=DC=2,即B(0,4),D(2,0).
可设直线BD的函数关系式:y=kx+b,将B、D的坐标代入,得到关于k、b的方程组,解之即可;
(3)因为M在直线BD上,所以可设M(a,-2a+4),因为△AMC为等腰三角形,所以需分情况讨论:
分三种情况:
①若AM=AC,利用两点间的距离公式可得AM2=a2+(-2a+4)2,因为AC2=16,所以可得到关于a的方程,解之即可;
②若MC=AC,利用两点间的距离公式可得MC2=(4-a)2+(-2a+4)2,AC2=16,所以可得到关于a的方程,解之即可;
③若AM=MC,利用两点间的距离公式可得AM2=a2+(-2a+4)2,MC2=(4-a)2+(-2a+4)2,a2+(-2a+4)2=(4-a)2+(-2a+4)2解之即可,又因M5(2,0)点在AC上,构不成三角形,所以应舍去.
解答: 解:(1)(4分)
解:(1)(4分)
正确画出平行四边形ABCP. (2分)
叙述画图过程合理. (4分)
方法一:在直线BD上取一点P,使PD=BD
连接AP,PC. (1分)
所以四边形ABCP是所画的平行四边形. (2分)
方法二:过A画AP∥BC,交直线BD于P,
连接PC. (1分)
所以四边形ABCP是所画的平行四边形. (2分)
(2)(4分)
∵AB=AC=4,BD是AC边上的中线,
∴AD=DC=2.
∴B(0,4),D(2,0). (2分)
设直线BD的函数关系式:y=kx+b,
得 解得
解得 . (3分)
. (3分)
∴直线BD的函数关系式:y=-2x+4. (4分)
(3)(6分)
设M(a,-2a+4). (2分)
分三种情况:
①AM=AC.
∵AM2=a2+(-2a+4)2,AC2=16.
∴a2+(-2a+4)2=16.解得 .
.
∴M1(0,4), . (3分)
. (3分)
②MC=AC.
∵MC2=(4-a)2+(-2a+4)2,AC2=16.
∴(4-a)2+(-2a+4)2=16.
解得 .
.
∴M3(4,-4), . (4分)
. (4分)
③AM=MC.
∵AM2=a2+(-2a+4)2,MC2=(4-a)2+(-2a+4)2,∴a2+(-2a+4)2=(4-a)2+(-2a+4)2,解得a5=2.
∴M5(2,0),这时M5点在AC上,构不成三角形,舍去. (5分)
综上所述,在直线BD上存在四点,即M1(0,4), ,M3(4,-4),
,M3(4,-4), 符合题意. (6分)
符合题意. (6分)
点评:本题主要考查待定系数法求函数的解析式和两点间的距离公式,解决这类问题常用到分类讨论、数形结合、方程和转化等数学思想方法,另外要注意答案的合理性.
即可得到BD=CD.利用对角线互相平分的四边形是平行四边形可知四边形ABCP是所画的平行四边形;
(2)因为AB=AC=4,BD是AC边上的中线,所以可得到AD=DC=2,即B(0,4),D(2,0).
可设直线BD的函数关系式:y=kx+b,将B、D的坐标代入,得到关于k、b的方程组,解之即可;
(3)因为M在直线BD上,所以可设M(a,-2a+4),因为△AMC为等腰三角形,所以需分情况讨论:
分三种情况:
①若AM=AC,利用两点间的距离公式可得AM2=a2+(-2a+4)2,因为AC2=16,所以可得到关于a的方程,解之即可;
②若MC=AC,利用两点间的距离公式可得MC2=(4-a)2+(-2a+4)2,AC2=16,所以可得到关于a的方程,解之即可;
③若AM=MC,利用两点间的距离公式可得AM2=a2+(-2a+4)2,MC2=(4-a)2+(-2a+4)2,a2+(-2a+4)2=(4-a)2+(-2a+4)2解之即可,又因M5(2,0)点在AC上,构不成三角形,所以应舍去.
解答:
 解:(1)(4分)
解:(1)(4分)正确画出平行四边形ABCP. (2分)
叙述画图过程合理. (4分)
方法一:在直线BD上取一点P,使PD=BD
连接AP,PC. (1分)
所以四边形ABCP是所画的平行四边形. (2分)
方法二:过A画AP∥BC,交直线BD于P,
连接PC. (1分)
所以四边形ABCP是所画的平行四边形. (2分)
(2)(4分)
∵AB=AC=4,BD是AC边上的中线,
∴AD=DC=2.
∴B(0,4),D(2,0). (2分)
设直线BD的函数关系式:y=kx+b,
得
 解得
解得 . (3分)
. (3分)∴直线BD的函数关系式:y=-2x+4. (4分)
(3)(6分)
设M(a,-2a+4). (2分)
分三种情况:
①AM=AC.
∵AM2=a2+(-2a+4)2,AC2=16.
∴a2+(-2a+4)2=16.解得
 .
.∴M1(0,4),
 . (3分)
. (3分)
②MC=AC.
∵MC2=(4-a)2+(-2a+4)2,AC2=16.
∴(4-a)2+(-2a+4)2=16.
解得
 .
.∴M3(4,-4),
 . (4分)
. (4分)③AM=MC.
∵AM2=a2+(-2a+4)2,MC2=(4-a)2+(-2a+4)2,∴a2+(-2a+4)2=(4-a)2+(-2a+4)2,解得a5=2.
∴M5(2,0),这时M5点在AC上,构不成三角形,舍去. (5分)
综上所述,在直线BD上存在四点,即M1(0,4),
 ,M3(4,-4),
,M3(4,-4), 符合题意. (6分)
符合题意. (6分)点评:本题主要考查待定系数法求函数的解析式和两点间的距离公式,解决这类问题常用到分类讨论、数形结合、方程和转化等数学思想方法,另外要注意答案的合理性.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
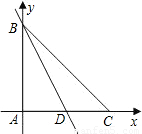
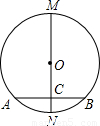
 BC;
BC; 的度数.
的度数.