题目内容
如图,在□ABCD中,BC=10,F为AD中点,CE⊥AB于点E,设∠B=![]()
![]()
⑴ 当![]() 时,求CE的长;
时,求CE的长;
⑵ 当![]() 时,
时,
① 连接CF并延长,交BA的延长线于点G,过点F做FH∥AB交BC于H,
求证:∠EFD=3∠AEF
② 若AB=5,当![]() 取最大值时,求tan∠DCF的值.
取最大值时,求tan∠DCF的值.

(1)解:∵CE⊥AB
∴∠BEC=90°
又∵∠a=60°
∴∠ECB=180°-∠BEC-∠a= 180°-90°-60°=30°
又∵∠a=60°
∴EB=![]() CB=5
CB=5
∴CE=![]()
 又∵CE⊥AB
又∵CE⊥AB
∴∠CEA=90![]()
∴EF=![]() GC=FC
GC=FC
又∵FH∥AB,CE⊥AB
∴CE⊥FH ∠EFH=∠AEF
∴∠EFH=∠CFH
又∵FH∥AB,AB∥CD,AD∥BC
∴四边形CDFH是平行四边形
∴FD=CH,FH=CD
又∵FC=CF
(2)①证明:∵F是AD的中点 ∴△FCH![]() △CFD(SSS)
△CFD(SSS)
∴AF=DF ∴∠CFD=∠CFH
又∵四边形ABCD是平行四边形 ∴∠AEF=∠EFH=∠HFC
∴AB∥CD AD∥BC =∠CFD
∴∠G=∠DCF ∠GAF=∠D ∴∠EFD=∠EFH+∠HFC
又∵在△AFG和△DFC中 +∠CFD=3∠AEF

∴△AFG![]() △DFC(AAS)
△DFC(AAS)
| ∴GF=CF (2)②设EB=x, ∵四边形ABCD是平行四边形 ,AB=5 ∴CD=AB=5 又∵△AFG ∴GA=CD=5, ∴GE=GB-BE=AB+AG=5+5-x=10-x ∴Rt△BCF中,CE 又∵CF= ∴CF ∴CE ∴当x= ∴tan∠DCF= |

 如图,在?ABCD中,对角线AC、BD相交于点O,AB=
如图,在?ABCD中,对角线AC、BD相交于点O,AB=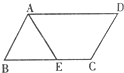 18、如图,在?ABCD中,∠A的平分线交BC于点E,若AB=10cm,AD=14cm,则EC=
18、如图,在?ABCD中,∠A的平分线交BC于点E,若AB=10cm,AD=14cm,则EC=
 (2011•犍为县模拟)甲题:已知关于x的一元二次方程x2=2(1-m)x-m2的两实数根为x1,x2.
(2011•犍为县模拟)甲题:已知关于x的一元二次方程x2=2(1-m)x-m2的两实数根为x1,x2.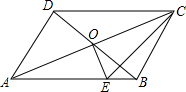 如图,在?ABCD中,∠ADB=90°,CA=10,DB=6,OE⊥AC于点O,连接CE,则△CBE的周长是
如图,在?ABCD中,∠ADB=90°,CA=10,DB=6,OE⊥AC于点O,连接CE,则△CBE的周长是