题目内容
【题目】如图,一次函数y=kx+b与反比例函数y=![]() (x>0)的图象交于A(m,6),B(3,n)两点.
(x>0)的图象交于A(m,6),B(3,n)两点.
(1)求一次函数的解析式;
(2)根据图象直接写出kx+b-![]() <0时x的取值范围;
<0时x的取值范围;
(3)求△AOB的面积.
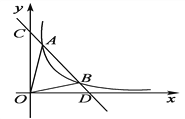
【答案】(1)这个函数的解析式为![]() ;(2)0<x<1或x>3;(3)8
;(2)0<x<1或x>3;(3)8
【解析】试题分析:(1)先把![]() 点坐标代入
点坐标代入![]() 求出
求出![]() 的值;然后将其分别代入一次函数解析式,列出关于系数
的值;然后将其分别代入一次函数解析式,列出关于系数![]() 的方程组,通过解方程组求得它们的值即可;
的方程组,通过解方程组求得它们的值即可;
(2)根据图象可以直接写出答案;
(3)直线![]() 交
交![]() 轴于D点,交
轴于D点,交![]() 轴于
轴于![]() 点.根据
点.根据![]() ,由三角形的面积公式可以直接求得结果.
,由三角形的面积公式可以直接求得结果.
试题解析:(1)∵点A(m,6),B(3,n)两点在反比例函数![]() (x>0)的图象上,
(x>0)的图象上,
∴m=1,n=2,
即A(1,6),B(3,2).
又∵点A(m,6),B(3,n)两点在一次函数y=kx+b的图象上,
∴![]()
解得![]()
则该一次函数的解析式为:y=2x+8;
(2)根据图象可知使kx+b<6x成立的x的取值范围是0<x<1或x>3;
(3)直线AB交x轴于D点,交![]() 轴于
轴于![]() 点.
点.
令![]() 得
得![]() 即
即![]()
∵A(1,6),B(3,2),
∴![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某天早上,一辆交通巡逻车从A地出发,在东西向的马路上巡视,中午到达B地,如果规定向东行驶为正,向西行驶为负,行驶纪录如下:(单位:km)
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
+15 | -8 | +6 | +12 | -4 | +5 | -10 |
(1)B地在A地哪个方向,与A地相距多少千米?
(2)巡逻车在巡逻过程中,离开A地最远是多少千米?
(3)若每km耗油0.1升,问共耗油多少升?