Question

等腰△ABC内接于半径为5的⊙O，点O到底边BC的距离为3，则AB的长为________．

Answer 1

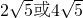
分析：分两种情况考虑：当三角形ABC为锐角三角形时，如图1所示，过A作AD垂直于BC，根据题意得到AD过圆心O，连接OB，在直角三角形OBD中，由OB与OD长，利用勾股定理求出BD的长，在直角三角形ABD中，利用勾股定理即可求出AB的长；当三角形ABC为钝角三角形时，同理求出AB的长，综上即可得到所有满足题意AB的长．
解答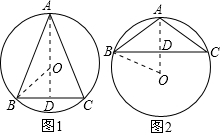：解：分两种情况考虑：当△ABC为锐角三角形时，如图1所示，
过A作AD⊥BC，由题意得到AD过圆心O，连接OB，
∵OD=3，OB=5，
∴在Rt△OBD中，根据勾股定理得：BD=4，
在Rt△ABD中，AD=AO+OD=8，BD=4，
根据勾股定理得：AB=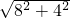=4；
当△ABC为锐角三角形时，如图2所示，
过A作AD⊥BC，由题意得到AD延长线过圆心O，连接OB，
∵OD=3，OB=5，
∴在Rt△OBD中，根据勾股定理得：BD=4，
在Rt△ABD中，AD=AO-OD=2，BD=4，
根据勾股定理得：AB==2，
综上，AB=2或4．
故答案为：2或4
点评：此题考查了垂径定理，勾股定理，利用了分类讨论的思想，熟练掌握垂径定理是解本题的关键．