Question

【题目】如图，直线，垂足为O，直线PQ经过点O，且点B在直线l上，位于点O下方，点C在直线PQ上运动连接BC过点C作，交直线MN于点A，连接点A、C与点O都不重合．

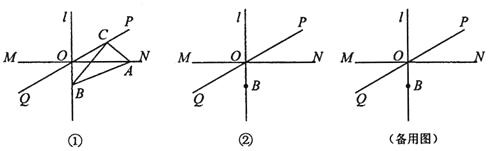
小明经过画图、度量发现：在中，始终有一个角与相等，这个角是________________；

当时，在图中画出示意图并证明；

探索和之间的数量关系，并说明理由．

Answer 1

【答案】（1）；（2）证明见解析；（3）和的数量关系是相等或互补，证明见解析.

【解析】（1）经测量可知，∠ABC=∠PON=30°;

（2）由BC∥MN可求∠OBC=90°,又因∠ACB=90°,所以∠OBC+∠ACB=180°,由同旁内角互补两直线平行可证结论成立；

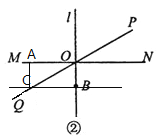
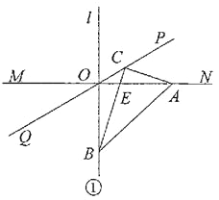
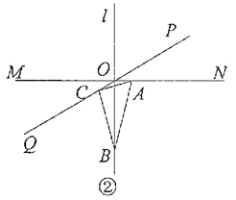
（3）分两种情况求解，如图1，由三角形内角和可知∠OCB=∠OAB;如图2，由四边形的内角和，结合已知条件可证∠OCB与∠OAB互补.

如图所示：

，

，

，

，

，

，

．

如图，设BC与OA相交于点E，

在和中，

，，

又，，

；

如图

，

，

，

在四边形ABCO中，，

即和互补，

和的数量关系是相等或互补．