题目内容
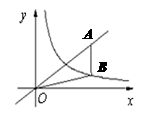
如图,一次函数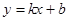 的图象与反比例函数
的图象与反比例函数 的图象相交于A、B两点.
的图象相交于A、B两点.
(1)利用图中条件,求反比例函数与一次函数的关系式;
(2)根据图象写出使该一次函数的值大于该反比例函数的值的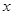 的取值范围;
的取值范围;
(3)过B点作BH垂直于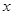 轴垂足为H,连接OB,在
轴垂足为H,连接OB,在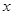 轴是否存在一点P(不与点O重合),使得以P、B、H为顶点的三角形与△BHO相似;若存在,直接写出点P的坐标;不存在,说明理由。
轴是否存在一点P(不与点O重合),使得以P、B、H为顶点的三角形与△BHO相似;若存在,直接写出点P的坐标;不存在,说明理由。
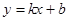 的图象与反比例函数
的图象与反比例函数 的图象相交于A、B两点.
的图象相交于A、B两点.(1)利用图中条件,求反比例函数与一次函数的关系式;
(2)根据图象写出使该一次函数的值大于该反比例函数的值的
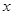 的取值范围;
的取值范围;(3)过B点作BH垂直于
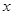 轴垂足为H,连接OB,在
轴垂足为H,连接OB,在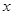 轴是否存在一点P(不与点O重合),使得以P、B、H为顶点的三角形与△BHO相似;若存在,直接写出点P的坐标;不存在,说明理由。
轴是否存在一点P(不与点O重合),使得以P、B、H为顶点的三角形与△BHO相似;若存在,直接写出点P的坐标;不存在,说明理由。
(1)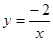 ,
,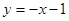 (2)
(2)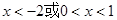 (3)存在,P1(2,0) P2(5,0) P3(-3,0)
(3)存在,P1(2,0) P2(5,0) P3(-3,0)
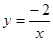 ,
,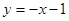 (2)
(2)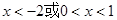 (3)存在,P1(2,0) P2(5,0) P3(-3,0)
(3)存在,P1(2,0) P2(5,0) P3(-3,0)解:(1)∵点A(-2,1)在反比例函数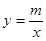 的图象上
的图象上
∴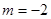 ,
,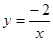 ………………………2分
………………………2分
又∵点B(1,n)也在函数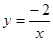 的图象上 ∴n=-2………………………3分
的图象上 ∴n=-2………………………3分
∵直线AB经过点A(-2,1)和B(1,-2)
∴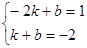 解得
解得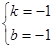 ∴
∴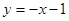 ………………………4分
………………………4分
(2)由图象知当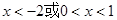 时该一次函数大于该反比例函数的值……………6分
时该一次函数大于该反比例函数的值……………6分
(3)存在,P1(2,0) P2(5,0) P3(-3,0) …………10分
(1)根据题意先求得m,再求出n,然后代入y=kx+b求得k、b即可;
(2)要使一次函数的值大于反比例函数的值,即使一次函数的图象在反比例函数的图象的上方时,再得出此时x的取值范围;
(3)利用相似三角形的性质,根据点P所在的不同位置分别讨论
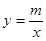 的图象上
的图象上∴
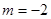 ,
,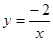 ………………………2分
………………………2分又∵点B(1,n)也在函数
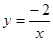 的图象上 ∴n=-2………………………3分
的图象上 ∴n=-2………………………3分∵直线AB经过点A(-2,1)和B(1,-2)
∴
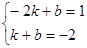 解得
解得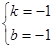 ∴
∴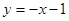 ………………………4分
………………………4分(2)由图象知当
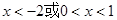 时该一次函数大于该反比例函数的值……………6分
时该一次函数大于该反比例函数的值……………6分(3)存在,P1(2,0) P2(5,0) P3(-3,0) …………10分
(1)根据题意先求得m,再求出n,然后代入y=kx+b求得k、b即可;
(2)要使一次函数的值大于反比例函数的值,即使一次函数的图象在反比例函数的图象的上方时,再得出此时x的取值范围;
(3)利用相似三角形的性质,根据点P所在的不同位置分别讨论

练习册系列答案
相关题目
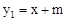 的图象与反比例函数
的图象与反比例函数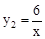 的图象交于A、B两点,.已知当
的图象交于A、B两点,.已知当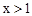 时,
时,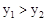 ;当
;当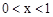 时,
时,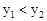 .
.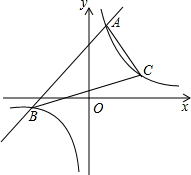
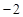 ,1),则此反比例函数表达式为_______
,1),则此反比例函数表达式为_______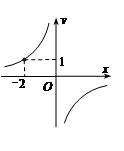
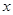 轴上,BC∥AO,AB⊥AO,过点C的双曲线
轴上,BC∥AO,AB⊥AO,过点C的双曲线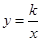 交OB于D,且
交OB于D,且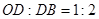 ,若△OBC的面积等于3,则k的值为 .
,若△OBC的面积等于3,则k的值为 .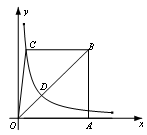
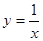 ,下列结论中不正确的是
,下列结论中不正确的是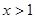 时,
时,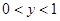
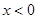 时,
时,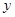 随着
随着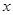 的增大而增大
的增大而增大 的图像上不重合的两点A(m1,n1),B(m2,n2),且
的图像上不重合的两点A(m1,n1),B(m2,n2),且 ,则函数
,则函数 的图像分布在第 象限.
的图像分布在第 象限.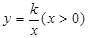 上一点,直线AB平行于
上一点,直线AB平行于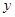 轴交直线
轴交直线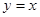 于点A,若
于点A,若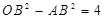 ,则
,则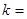 .
.