题目内容
 4、如图,以△ABC的三边为边在BC的同一侧分别作三个等边三角形,即△ABD、△BCE、△ACF.
4、如图,以△ABC的三边为边在BC的同一侧分别作三个等边三角形,即△ABD、△BCE、△ACF.(1)四边形ADEF是
平行四边形
;(2)当△ABC满足条件
AB=AC
时,四边形ADEF为菱形;(3)当△ABC满足条件
AB=AC=BC
时,四边形ADEF不存在.分析:(1)先证明△ABC≌△DBE,△ABC≌△FEC,则DE=AC=AF,FE=AB=AD,则四边形ADEF是个平行四边形;
(2)当AB=AC时,四边形ADEF为菱形;
(3)当AB=AC=BC时,四边形ADEF不存在.
(2)当AB=AC时,四边形ADEF为菱形;
(3)当AB=AC=BC时,四边形ADEF不存在.
解答:解:(1)四边形ADEF是个平行四边形在△ABC和△DBE中,
∵BC=BE,BA=BD,∠DBE=∠ABC(与∠ABE之和都等于60°),
∴△ABC≌△DBE,
∴DE=AC,
在△ABC和△FEC中,
∵BC=EC,CA=CF,∠ACB=∠FCE(都为60°角与=∠ACE之和),
∴△ABC≌△FEC,
∴FE=AB,
∴DE=AC=AF,FE=AB=AD,
∴四边形ADEF是个平行四边形;
(2)当△ABC为等腰三角形并且不是等边三角形时,即AB=AC时,
由第(1)题中可知四边形ADEF的四边都相等,此时四边形ADEF是菱形;
(3)当△ABC为等边三角形时,即AB=AC=BC时,四边形ADEF中的A点与E点重合,
此时以A、D、E、F为顶点的四边形不存在.
∵BC=BE,BA=BD,∠DBE=∠ABC(与∠ABE之和都等于60°),
∴△ABC≌△DBE,
∴DE=AC,
在△ABC和△FEC中,
∵BC=EC,CA=CF,∠ACB=∠FCE(都为60°角与=∠ACE之和),
∴△ABC≌△FEC,
∴FE=AB,
∴DE=AC=AF,FE=AB=AD,
∴四边形ADEF是个平行四边形;
(2)当△ABC为等腰三角形并且不是等边三角形时,即AB=AC时,
由第(1)题中可知四边形ADEF的四边都相等,此时四边形ADEF是菱形;
(3)当△ABC为等边三角形时,即AB=AC=BC时,四边形ADEF中的A点与E点重合,
此时以A、D、E、F为顶点的四边形不存在.
点评:本题考查了平行四边形、菱形的判定以及等边三角形的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 25、如图,以△ABC的三边为边,在BC的同一侧分别作三个等边三角形,△ABD,△BCE和△ACF.
25、如图,以△ABC的三边为边,在BC的同一侧分别作三个等边三角形,△ABD,△BCE和△ACF. 16、如图,以△ABC的三边为边,在BC的同侧分别另作三个等边三角形,即△ABD,△BCE,△ACF.
16、如图,以△ABC的三边为边,在BC的同侧分别另作三个等边三角形,即△ABD,△BCE,△ACF. 如图,以△ABC的三顶点为圆心,半径为1,作两两不相交的扇形,则图中三个扇形面积之和是
如图,以△ABC的三顶点为圆心,半径为1,作两两不相交的扇形,则图中三个扇形面积之和是 如图,以△ABC的各边为边分别向外作正方形,所得到的三个正方形的面积分别为S1=36,S2=64,S3=100,则△ABC的面积是( )
如图,以△ABC的各边为边分别向外作正方形,所得到的三个正方形的面积分别为S1=36,S2=64,S3=100,则△ABC的面积是( )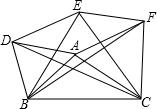 如图,以△ABC的三边为边在BC的同一侧分别作三个等边三角形,即△ABD、△BCE、△ACF
如图,以△ABC的三边为边在BC的同一侧分别作三个等边三角形,即△ABD、△BCE、△ACF