题目内容
如图所示,在平面上有一半径为1 cm的圆定点A,OA="4" cm.以点A为旋转中心,使圆O分别顺时针旋转90°,逆时针旋转60°,得到圆B和圆C,作出这两个圆.
(1)试问圆B或圆C的圆心与圆O的圆心O的距离是多少?
(2)试问圆B和圆C的圆心的距离是多少?

(1)试问圆B或圆C的圆心与圆O的圆心O的距离是多少?
(2)试问圆B和圆C的圆心的距离是多少?

(1) cm,4cm;(2)
cm,4cm;(2) cm.
cm.
 cm,4cm;(2)
cm,4cm;(2) cm.
cm.试题分析:(1)根据旋转的性质得出对应点坐标进而得出答案,利用勾股定理以及等边三角形的判定与性质得出答案;
(2)作CD⊥BA延长线于点D,连接BC,首先得出CD的长,进而得出AD的长,再利用勾股定理得出答案.
试题解析:(1)如图作出圆B和圆C,
∵∠OAB=90°,AO=AB=4cm,∴OB=
 cm.
cm.∵AO=AC,∠OAC=60°,∴△AOC是等边三角形.∴CO=4cm.
∴圆B或圆C的圆心与圆O的圆心O的距离分别是:
 cm,4cm;
cm,4cm;(2)作CD⊥BA延长线于点D,连接BC,
∵∠OAC=60°,∠OAB=90°,∴∠CAD=30°.
∴CD=
 AC=2,AD=ACsin60°=
AC=2,AD=ACsin60°= .∴BD=
.∴BD= .
.∴
 (cm).
(cm).
练习册系列答案
相关题目
 .
.

 ,若存在,求出所有符合条件的m的值,若不存在,请说明理由.
,若存在,求出所有符合条件的m的值,若不存在,请说明理由.

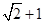 B.
B. C.
C. D.
D.
