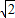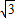题目内容
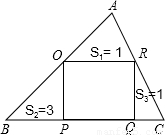
如图，正方形OPQR内接于△ABC．已知△AOR、△BOP和△CRQ的面积分别是S1=1，S2=3和S3=1，那么，正方形OPQR的边长是（ ）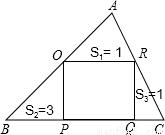
A．
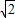
B．
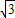
C．2
D．3
【答案】分析：先设正方形OPQR的边长为，求得△ABC的高，然后分别求出BP、QC，利用三角形的面积即可求得正方形OPQR的边长．
解答：解：设正方形OPQR的边长为x，
则△ABC的面积为：x2+3+1+1=x2+5，
三角形高为正方形OPQR的边长x加上△AOR的高，即
+x，
底为：BP+x+QC，由S2=3和S3=1得，BP=
，QC=
，
则底为：
+x+
，
所以x2+5=（
+x+
）（
+x）×
，
解得x=2．
故选C．
点评：此题主要考查学生对正方形的性质的理解与应用，主要利用三角形的面积求得高和边长，这是解答此题的关键．
解答：解：设正方形OPQR的边长为x，
则△ABC的面积为：x2+3+1+1=x2+5，
三角形高为正方形OPQR的边长x加上△AOR的高，即
+x，底为：BP+x+QC，由S2=3和S3=1得，BP=
，QC=，则底为：
+x+，所以x2+5=（
+x+）（+x）×，解得x=2．
故选C．
点评：此题主要考查学生对正方形的性质的理解与应用，主要利用三角形的面积求得高和边长，这是解答此题的关键．
练习册系列答案
相关题目
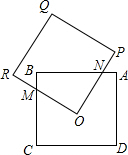如图所示，两个边长都为2的正方形ABCD和OPQR，如果O点正好是正方形ABCD的中心，而正方形OPQR可以绕O点旋转，那么它们重叠部分的面积为（ ）
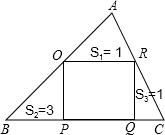如图，正方形OPQR内接于△ABC．已知△AOR、△BOP和△CRQ的面积分别是S1=1，S2=3和S3=1，那么，正方形OPQR的边长是（ ）
如图，正方形OPQR内接于△ABC．已知△AOR、△BOP和△CRQ的面积分别是S1=1，S2=3和S3=1，那么，正方形OPQR的边长是
