题目内容
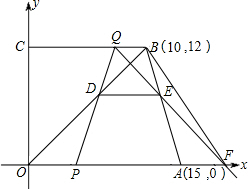
 如图,在直角梯形OABC中,AB∥OC,过B点的双曲线y=
如图,在直角梯形OABC中,AB∥OC,过B点的双曲线y=| k | x |
3
3
.分析:先设出点B和点C的坐标,再进一步表示出线段BC的中点D的坐标;根据反比例函数的解析式以及梯形的面积,即可求解.
解答:解:设B点的坐标是(m,n),点C的坐标是(p,0),则A(0,n),
∵D是BC的中点,
∴D的坐标是(
,
)
∵点D在函数y=
(k>0)的图象上,
∴k=xy=
•
=
,即(m+p)•n=4k①,
∵S梯形ABCO=6,
∴
(OC+AB)•OA=6,
×(m+p)×n=6②,
把①代入②得,
×4k=6,解得k=3.
故答案为:3.
∵D是BC的中点,
∴D的坐标是(
| m+p |
| 2 |
| n |
| 2 |
∵点D在函数y=
| k |
| x |
∴k=xy=
| m+p |
| 2 |
| n |
| 2 |
| n(m+p) |
| 4 |
∵S梯形ABCO=6,
∴
| 1 |
| 2 |
| 1 |
| 2 |
把①代入②得,
| 1 |
| 2 |
故答案为:3.
点评:本题考查的是反比例函数综合题及梯形的面积,熟知反比例函数y=
中,k=xy的特点是解答此题的关键.
| k |
| x |

练习册系列答案
相关题目
 动时间为t(单位:秒).
动时间为t(单位:秒).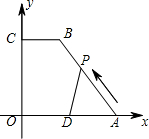 (10,0)、C(0,8),CB=4,D为OA中点,动点P自A点出发沿A→B→C→O的线路移动,速度为1个单位/秒,移动时间为t秒.
(10,0)、C(0,8),CB=4,D为OA中点,动点P自A点出发沿A→B→C→O的线路移动,速度为1个单位/秒,移动时间为t秒.
 单位,移动时间记为t秒.
单位,移动时间记为t秒. 如图,在直角梯形OABC中,AB∥OC,BC⊥x轴于点C,A(1,2),C(3,0).动点P从O点出发,沿x轴正方向以每秒1个单位长度的速度移动.过P点作PQ⊥直线OA,垂足为Q.设P点移动的时间为t秒(0<t≤7),△OPQ与直角梯形OABC重叠部分的面积为S.
如图,在直角梯形OABC中,AB∥OC,BC⊥x轴于点C,A(1,2),C(3,0).动点P从O点出发,沿x轴正方向以每秒1个单位长度的速度移动.过P点作PQ⊥直线OA,垂足为Q.设P点移动的时间为t秒(0<t≤7),△OPQ与直角梯形OABC重叠部分的面积为S.