题目内容
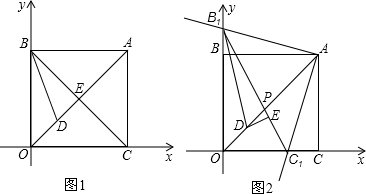
如图1,在正方形ABOC中,BD平分∠OBC,交OA于点D.(1)若正方形ABOC的边长为2,对角线BC与OA相交于点E.则:
①BC的长为
(2)如图2,当直角∠BAC绕着其顶点A顺时针旋转时,角的两边分别与x轴正半轴、y轴正半轴交于点C1和B1,连接B1C1交OA于P.B1D平分∠OB1C1,交OA于点D,过点D作DE⊥B1C1,垂足为E,请猜想线段OB、B1C1、DE三者之间的数量关系,并证明你的猜想;
(3)在(2)的条件下,当B1E=6,C1E=4时,求直线B1D的解析式.
分析:(1)①根据正方形的性质即可求得对角线BC的长;②BD平分∠OBC,经计算可知△ABD为等腰三角形,所以可知道AD长度,即可求得DE长度;③经计算可知线段OB、BC、DE的长的关系为OB=
BC+DE;
(2)猜想线段OB、B1C1、DE的长的关系为OB=
B1C1+DE,利用相似三角形即可证明;
(3)根据(2)中条件求出点D和点的B1坐标,代入即可求出直线B1D的解析式.
| 1 |
| 2 |
(2)猜想线段OB、B1C1、DE的长的关系为OB=
| 1 |
| 2 |
(3)根据(2)中条件求出点D和点的B1坐标,代入即可求出直线B1D的解析式.
解答:解:(1)①2
;(1分)
②2-
;(3分)
③线段OB、BC、DE的长的关系为OB=
BC+DE(5分)
注:只要符合三条线段长度关系的式子都对.
(2)猜想线段OB、B1C1、DE的长的关系为OB=
B1C1+DE.(6分)
证明如下:过点D作DF⊥OB于F.
∵∠BAC=∠B1AC1=90°,
∴∠B1AB=∠C1AC.
又∵AB=AC,∠B1BA=∠C1CA=90°,
∴△B1BA≌△C1CA(ASA),(7分)
∴B1A=C1A,
∴AB1=
B1C1.
∵∠B1DA=∠AOB+∠OB1D=45°+∠OB1D,
∠DB1A=∠DB1C1+∠AB1C1=45°+∠DB1C1,
∵∠OB1D=∠DB1C1,
∴∠B1DA=∠DB1A,
∴AD=AB1=
B1C1(8分)
∴OD=
DF=
DE且AO=
OB,
∴AD+OD=
OB,
∴
B1C1+
DE=
OB,
∴OB=
B1C1+DE.
(3)∵B1E=6,C1E=4,
∴B1C1=10.
由(2)得OB=5+DE=5+DF,(10分)
∴BF=5.
∵B1F=B1E=6,
∴B1B=1,AB1=5
,
∴AB=OB=
=7,
∴DE=2.
∴D的坐标为(2,2),B1的坐标为(0,8),(11分)
∴直线B1D的解析式y=-3x+8.(12分)
| 2 |
②2-
| 2 |
③线段OB、BC、DE的长的关系为OB=
| 1 |
| 2 |
注:只要符合三条线段长度关系的式子都对.
(2)猜想线段OB、B1C1、DE的长的关系为OB=
| 1 |
| 2 |
证明如下:过点D作DF⊥OB于F.
∵∠BAC=∠B1AC1=90°,
∴∠B1AB=∠C1AC.
又∵AB=AC,∠B1BA=∠C1CA=90°,
∴△B1BA≌△C1CA(ASA),(7分)
∴B1A=C1A,
∴AB1=
| ||
| 2 |
∵∠B1DA=∠AOB+∠OB1D=45°+∠OB1D,
∠DB1A=∠DB1C1+∠AB1C1=45°+∠DB1C1,
∵∠OB1D=∠DB1C1,
∴∠B1DA=∠DB1A,
∴AD=AB1=
| ||
| 2 |
∴OD=
| 2 |
| 2 |
| 2 |
∴AD+OD=
| 2 |
∴
| ||
| 2 |
| 2 |
| 2 |
∴OB=
| 1 |
| 2 |
(3)∵B1E=6,C1E=4,

∴B1C1=10.
由(2)得OB=5+DE=5+DF,(10分)
∴BF=5.
∵B1F=B1E=6,
∴B1B=1,AB1=5
| 2 |
∴AB=OB=
(5
|
∴DE=2.
∴D的坐标为(2,2),B1的坐标为(0,8),(11分)
∴直线B1D的解析式y=-3x+8.(12分)
点评:本题主要考查对于一次函数的综合应用以及相似三角形的掌握.

练习册系列答案
相关题目

 构造一个与上述命题类似的正确命题并加以证明.
构造一个与上述命题类似的正确命题并加以证明. 26、如图1,在正方形ABCD中,若点E是△DBC内的一点,且DE=DC,BE=CE.
26、如图1,在正方形ABCD中,若点E是△DBC内的一点,且DE=DC,BE=CE.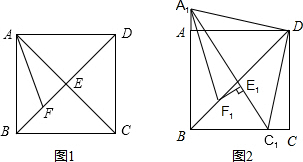 如图1,在正方形ABCD中,对角线AC与BD相交于点E,AF平分∠BAC,交BD于点F.
如图1,在正方形ABCD中,对角线AC与BD相交于点E,AF平分∠BAC,交BD于点F.