题目内容
在平面直角坐标系中，设点P到原点的距离为
(希腊字母读作“柔”)，OP与X轴的正方向的夹角
，则用[
]表示点P的极坐标。显然点P的坐标和它的极坐标存在一一对应关系。如点P的坐标(1,1)的极坐标为P[
],则极坐标Q[
]的坐标为
(希腊字母读作“柔”)，OP与X轴的正方向的夹角，则用[]表示点P的极坐标。显然点P的坐标和它的极坐标存在一一对应关系。如点P的坐标(1,1)的极坐标为P[],则极坐标Q[]的坐标为 
找到与x轴的正方向成120°的角，且距离原点为2
的点的坐标即可．
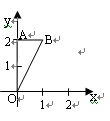
解：如图．
∠QOB=120°，OQ=2，
∴∠AOQ=60°，
∴OA=，AQ=3，
∴极坐标Q[2，120°]的坐标为（-，3）或（-，-3）．
的点的坐标即可．解：如图．
∠QOB=120°，OQ=2
，∴∠AOQ=60°，
∴OA=
，AQ=3，∴极坐标Q[2
，120°]的坐标为（-，3）或（-，-3）．
练习册系列答案
新课标同步训练系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
），教学楼所在位置的坐标为（1，3），那么语音室所在位置的坐标为 ．